Категории публикаций
Публикации - Инженерные аспекты
Двойной корреляционный прием симметричного импульса в условиях АБГШ
13.12.2010
Крамаренко А.В.
Оптимальное когерентное (двоичное) пороговое обнаружение слабого сигнала в аддитивном шуме определяется главным образом квадратным корнем из отношения сигнал/шум на входе по мощности, а само устройство для обнаружения должно определять усредненную обобщенную взаимную корреляцию принятых данных с сигналом.
Дэвид Миддлтон
.
Оптимальное обнаружение единичного импульса в присутствии шума состоит, согласно современным представлениям, из двух частей.
- Оптимальная фильтрация, представляющая собой свертку принятого сигнала с его инвертированной во времени копией.
- Нелинейное преобразование (в виде принятия решения: сигнал есть или его нет) пороговым обнаружителем с минимальным байесовским риском, либо устройством, обнаруживающим экстремум отклика идеального фильтра.
Рассмотрим классический пример обнаружения симметричного прямоугольного видеоимпульса. Используем специально написанную программу для получения экспериментальных результатов выделения импульса на фоне белого гауссовского шума.
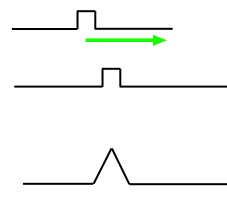
Рис. 1. Свертка сигнала с его копией в случае нулевого шума.
В соответствии с теорией отклик системы представляет собой импульс треугольной формы, ширина основания которого вдвое шире основания входного импульса.
При наличии шума результат оптимальной фильтрации получается следующим:
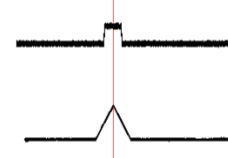
Рис.2. АБГШ с амплитудой много меньше сигнала при 1000 кратном наложении изображений.
В случае увеличения уровня шума обнаружение импульса будет все более затруднено, возрастет вероятность ошибок первого и второго рода.
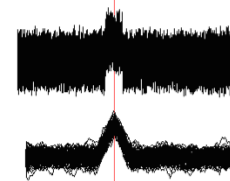
Рис.3. Уровень шума сравним с уровнем сигнала.
Для того чтобы оценить эффективность пороговых обнаружителей любого типа (а именно они чаще всего применяются в реальной технике), используем стандартный метод глазковых диаграмм. Рассмотрим предельный случай, когда обнаружение находится на грани появления ошибок.
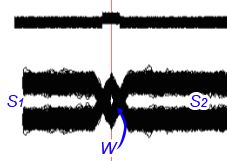
Рис. 4. Глазковая диаграмма выхода оптимального фильтра. 1000 итераций.
Очевидно, что для нашего случая отсутствие ошибок обнаружения будет наблюдаться тогда и только тогда, когда существует незакрытый глазок W, а щели S1 и S2 проходимы по всей длине.
Покажем, что при дальнейшем увеличении уровня шума безошибочное обнаружение импульса с помощью данного алгоритма невозможно при любой установке порога.
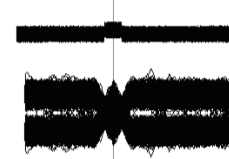
Рис.5. Уровень шума повышен на 3dB. Глазок отсутствует, щели непроходимы. Хорошо видно, что при условии любого порога будут возникать ошибки, как первого, так и второго рода.
Очевидно, что в данном случае достигнут теоретический предел возможности безошибочного обнаружения импульса.
Допустим, однако, что мы использовали не все возможности оптимизации приемного устройства. В частности, нами не учтен тот факт, что принимаемый импульс симметричен. Т.е. если отразить его обе половины друг на друга относительно оси симметрии, то мы вправе надеяться, что соотношение сигнал/некогерентный относительно данного отражения шум улучшится на 3dB (т.к. суммирование двух половин сигнала эквивалентно когерентному накоплению двух реализаций этого же сигнала).
Покажем это эффект на наглядном примере. Пусть есть фотография, где изображение симметрично относительно вертикальной оси. Тогда каждая строка изображения будет повторяться (с инверсией, разумеется) после оси симметрии.

Рис.6. Сделаем портрет Норберта Винера осесимметричным относительно красной линии, т.е. используем только одну половину изображения.

Рис.7. Добавим АБГШ, причем шум не имеет симметрии, которой обладает исходный портрет.

Рис.8. С учетом инверсии наложим правую половину портрета на левую. Видно, что зашумленность левой части портрета уменьшилась.

Рис. 9. Перемножим полученное изображение на прототип, т.е. выполним операцию, близкую оптимальной фильтрации при приеме импульса.
Очевидно, что в данном случае левая часть портрета восстановлена более правильно т.к. имеет улучшенное на 3dB соотношение сигнал/шум.
В нашем случае подобный метод бессмысленно применять к входному сигналу, т.к. положение оси симметрии (т.е. момента поступления импульса) нам априори неизвестно, более того, это является целью работы всей системы. Попытка использования такого метода приведет к «размножению» входных импульсов, расширению отклика системы во времени и нисколько не улучшит соотношения сигнал/шум после оптимальной фильтрации.
Но ничто не запрещает применить подобный метод к выходному сигналу при условии, что мы будем вычислять корреляционную функцию с его прототипом методом нормированной корреляции. Поясним: вычисляется пирсоновский коэффициент корреляции со скользящим окном, где сигналами являются отклик системы после оптимального фильтра (в нашем случае – треугольный сигнал) и прототип (т.е. тот же треугольный сигнал). При этом входной сигнал усредняется относительно оси симметрии, которая определяется как центр скользящего окна.
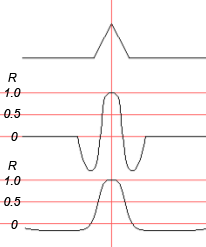
Рис.10. Пирсоновский сигнал для скользящего окна, равного по длительности входному треугольному импульсу (вторая кривая) и равного всей реализации (нижняя кривая).
Проведем эксперимент с обнаружением импульса в условиях АБГШ небольшого (относительно импульса) уровня.
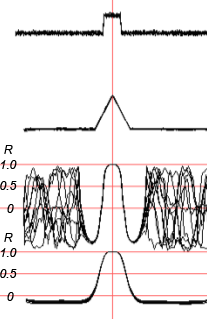
Рис.11. Для скользящего окна, равного по длительности ожидаемому импульсу, имеются постоянные ложные повышения R почти до 1.0. Однако в окрестностях импульса ошибки отсутствуют.
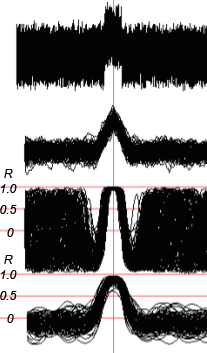
Рис. 12. Для случая высокого уровня шума видно, что пирсоновский сигнал вполне пригоден для порогового обнаружения импульса.
Покажем экспериментально, что предлагаемый метод приема симметричного импульса действительно обеспечивает работу при худших соотношениях сигнал/шум. Для этого применим глазковые диаграммы.

Рис.13. Оба обнаружителя работают без ошибок.

Рис. 14. Уровень шума повышен на 3dB по амплитуде. Безошибочно работает только предлагаемый обнаружитель.
Для того чтобы обеспечить сужение отклика системы можно использовать сигнал для окна, равного по длительности выходному импульсу системы, при условии, что коэффициент корреляции для окна, длительностью равной реализации, превысил уровень R=0.
В итоге можно рекомендовать следующее построение детектора: реализация сигнала, полученная после оптимальной фильтрации (в нашем случае 256 отсчетов) сравнивается (т.е. вычисляется коэффициент корреляции по формуле Пирсона) с прототипом, причем входной сигнал дополнительно обрабатывается следующим образом: симметричные относительно центра прототипа отсчеты входного сигнала усредняются. Если симметричный отсчет находится за пределами реализации, то операция не производится.
Такая же операция проводится и с «коротким» скользящим окном (в нашем случае 40 отсчетов при длительности входного сигнала 20 отсчетов). Получаются две кривые (нижние линии на рисунках 11 и 12). Их положительные значения (отрицательные обнуляются) перемножаются между собой, и мы имеем единственный выходной сигнал, описывающий степень подобия принятого сигнала эталону. Понятно, что происходит некоторая маргинотомия - «хвосты» реализации усекаются на длительность ожидаемого сигнала.
Позволю себе предложить назвать такое устройство двойным корреляционным детектором.
Рассмотрим работу детектора чуть более подробно.
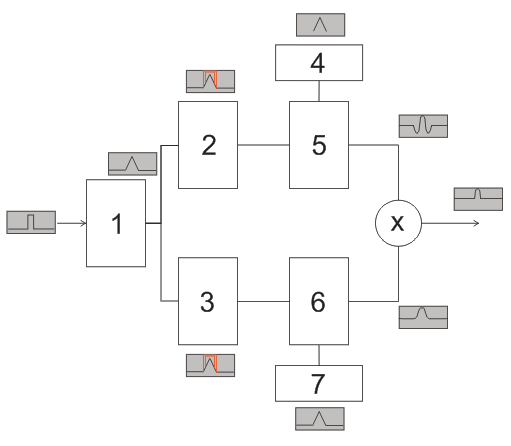
Рис.14а. Блок-схема двойного корреляционного детектора.
1 – оптимальный фильтр; 2,3 – блоки зеркального суммирования; 4,7 – прототипы сигналов; 5 – первый коррелятор: скользящее окно равно длительности импульса; 6 – второй коррелятор: скользящее окно равно реализации; Х – перемножитель.
1 – оптимальный фильтр; 2,3 – блоки зеркального суммирования; 4,7 – прототипы сигналов; 5 – первый коррелятор: скользящее окно равно длительности импульса; 6 – второй коррелятор: скользящее окно равно реализации; Х – перемножитель.
На выходе всей системы получается сигнал, представленный на рис.15.
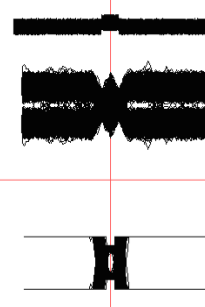
Рис.15. Глазковая диаграмма для предлагаемого детектора (внизу).В данном случае соотношение сигнал/шум не позволяет избегать ошибок при использовании стандартных пороговых устройств (диаграмма в середине).

Рис.16. Изменение выходного сигнала детектора в зависимости от входного соотношения сигнал/шум. Поведение устройства очень похоже на «захват частоты» обычным ЧМ детектором.
Обратим внимание, что выходной сигнал детектора не зависит от уровня входного и всегда находится в пределах 0…1. Т.е. система автоматической регулировки усиления может быть отключена (если будет обеспечен требуемый динамический диапазон).
Следует отметить также, что при когерентном накоплении сигналов т.н. «прожигании помехи» можно воспользоваться функцией усреднения не на входе, а на выходе детектора. В этом случае удается получить дополнительную информацию о соотношении сигнал/шум исходных последовательностей и, соответственно, прогнозировать минимально необходимое количество итераций накопления.
Следует отметить также, что при когерентном накоплении сигналов т.н. «прожигании помехи» можно воспользоваться функцией усреднения не на входе, а на выходе детектора. В этом случае удается получить дополнительную информацию о соотношении сигнал/шум исходных последовательностей и, соответственно, прогнозировать минимально необходимое количество итераций накопления.
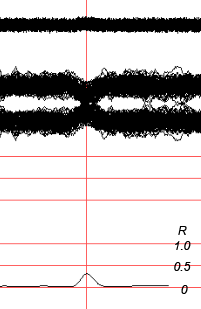
Рис.17. «Прожигание помехи» методом когерентного накопления 64-х реализаций. Обратим внимание, что уровень выходного сигнала детектора пропорционален входному (очень маленькому NB!) соотношению сигнал/шум.
Выводы:
- Предлагаемый двойной корреляционный детектор при приеме одиночного симметричного импульса в присутствии шумов дает выигрыш 3дБ по амплитуде и, соответственно, вдвое по мощности. Следует предполагать, что это преимущество будет наиболее востребовано в РЛС системах т.к. можно получить выигрыш, эквивалентный двукратному повышению мощности передатчика.
- Нормированный выходной сигнал, пропорциональный степени подобия принятого импульса эталонному, дает возможность вести оптимальное детектирование вне зависимости от уровня входного сигнала, чем выгодно отличается от пороговых обнаружителей.
- На базе предлагаемого устройства можно проектировать не только системы обнаружения, но и распознавания различных входных сигналов, для чего необходимо проводить сравнение не с одним, а с несколькими прототипами. В этом случае можно реализовать принцип оптимального приемника, не нуждающегося в системах АРУ.
- Понимая, что надо бы отправить все это в рецензируемое издание, и не имея никакого желания этого делать, надеюсь, что компетентные читатели помогут конструктивной критикой.
Категории:
- Войдите, чтобы оставлять комментарии
Адрес: Украина, 61057, Харьков, а/я 39,
тел./факс.: +38(050)0113940, +38(057)7290409.
E-mail: tredex@tredex-company.com
tredex.office@gmail.com
Комментарии
PSP
25.11.2011 - 19:27
Постоянная ссылка (Permalink)
Огромное человеческое спасибо за статью. Очень чуткий коррелятор. Я его исследовал со всех сторон, модифицировал, снизил сложность в сотни раз. Планируем использовать для обработки изображений со скоростью 500 кадров в секунду.