Использование априорной информации о сигнале в качестве основы корректирующих кодов

 

 Абсурдно, разумеется, оспаривать необходимость избыточности данных для реализации корректирующего кода. Однако, необходимо учитывать, что требуемая избыточность уже имеется в любом дискретизованном сигнале. Если, конечно, он обработан корректно.

 

Не подлежит сомнению, что применение любого квантователя требует выполнения условия Котельникова с некоторым запасом, определяемым величиной неидеальности реального ФНЧ системы дискретизации. Именно этот запас можно рассматривать как источник избыточной информации в сигнале. Иными словами, каждый следующий дискретный отсчет сигнала не может быть абсолютно независимым от предыдущих (т.к. он коррелирует с ними) и компоненты марковского процесса, обусловленные процедурой квантования, всегда присутствуют в передаваемой последовательности данных. Очевидно также, что для идеального ФНЧ характеристики потерянного дискретного отсчета могут быть вычислены с помощью сопоставления данных от функции sin(x)/x, примененной ко всем остальным цифровым данным реализации. Разумеется, речь идет о восстановленном на приемном конце исходном сигнале, а не о последовательности бит в линии.

 

 Предположим, что в передаваемом оцифрованном сигнале (обозначен черным цветом на рис.1) имеется единичный сбой, обусловленный импульсной помехой в линии. В этом случае один отсчет сигнала приобретает случайное значение. В то же время функция глобально заданного кубического сплайна (или другой интерполятор) будет давать в точке сбоя иное значение, не слишком отличающееся от истинного. Важнейшим фактом будет отличие принятого значения от интерполированного, полученного вследствие предсказаний вперед и назад. И еще более важным будет получение локального экстремума кривой, вычисленной как модуль разности истинных и предсказанных значений. Именно этот экстремум позволит обнаружить и скорректировать с приемлемой (определяемой условиями задачи и вычислительной сложностью) точностью исходный сигнал.

 

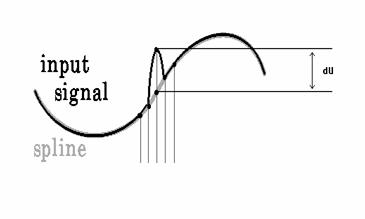
Рис. 1.

 

 Примем в качестве простейшего утверждения, что любой единичный сбой в передаваемом оцифрованном сигнале может быть скорректирован с точностью, определяемой скрытой избыточностью сигнала. Тогда ошибка корректировки (при идеальном интерполяторе) будет обусловлена только параметрами ФНЧ реального квантователя. В случае же предобработки сигнала перед подачей его в линию можно добиться практически любой требуемой точности корректировки. Естественно, предыскажения сигнала должны будут компенсироваться на приемном конце линии связи, т.е. необходимо использовать обратимое преобразование. Очевидно также, что такой метод не может быть применен для шумопонижения, фильтрации помех в исходном сигнале, улучшения соотношения сигнал/шум и т.п., он пригоден лишь для обнаружения и коррекции сбоев в цифровой линии связи.

 

 Попробуем с помощью реальных сигналов оценить эффективность метода коррекции. Учитывая неопределенность требований к точности восстановления и разнообразие методов оцифровки, будем использовать электрофизиологический сигнал с последующей визуальной оценкой и акустические сигналы с последующей экспертной оценкой качества звучания.

 

 Для сигнала электрокардиограммы и тестового ЛЧМ сигнала (график 1 рис.2) получим первую производную (график 2) и имитируем сбои в линии передачи (график 3 на рис.2). Восстановим с помощью предлагаемого алгоритма (в данном случае для замены потерянных отсчетов используется глобально заданный кубический сплайн) первую производную (график 4) и восстановим исходный сигнал (график 5).

 

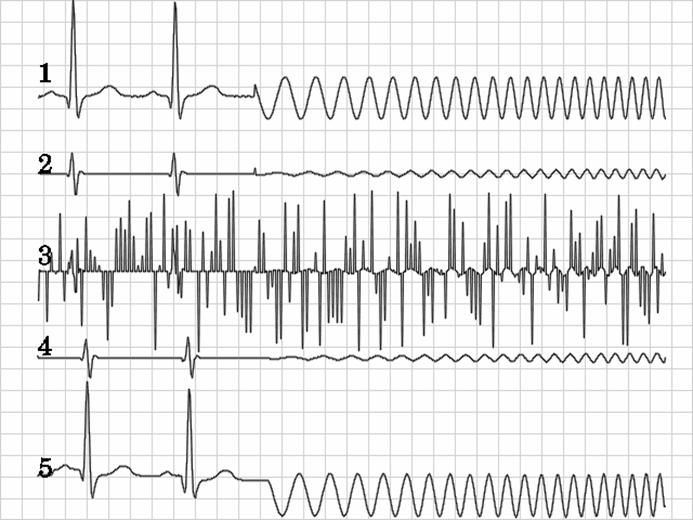
Рис.2

 

 Можно считать реконструкцию успешной, т.к. несмотря на весьма значительное количество сбоев, а также неизвестность частоты их следования, и электрокардиограмма и ЛЧМ сигнал восстановлены в виде, пригодном для визуального анализа, что и требовалось. Обратим внимание на режекцию компонента, возникшего в момент замены сигнала ЭКГ сигналом ЛЧМ. Очевидно, что исчезновение этого пика обусловлено тем, что он физически невозможен при использовании реального квантователя с ФНЧ. Т.е. удаленный системой выброс был подавлен в полном соответствии с базовой гипотезой – он имел такие же отклонения предсказанного от истинного значения, как и сбой в линии связи.

 

 Приведенная иллюстрация показывает, что произошло не полное восстановление потерянных в процессе передачи данных, а реконструкция с требуемой условиями задачи точностью. И если эта точность представляется недостаточной, то не будем забывать, что она обусловлена параметрами фильтра, обеспечивающего подавление эффекта маскировки частот при дискретизации. Очевидно также, что величина просачивания высокочастотных спектральных компонентов через половину частоты дискретизации, которая удовлетворяет пользователя в оцифрованном сигнале, определяет корректность апостериорной реконструкции. Как следствие – неправильно квантованный исходный сигнал будет восстановлен с большими погрешностями, чем корректно оцифрованный. Более того, даже при отсутствии сбоев в линии, система коррекции способна внести искажения в такой сигнал. И, само собой разумеется, что точность восстановления данных будет тем ниже, чем большее количество сбоев передачи прошло подряд, один за другим.

 

 Проверим корректность восстановления оцифрованных акустических сигналов, прошедших через линию связи с импульсными помехами. В файле signal.wav (871 kB) записан исходный речевой сигнал. В файле signal_8_noise.wav (871 kB) имитирована линия передачи со сбоями – каждый восьмой байт исходного сигнала заменен случайными значениями. Файл restore8_iter1.wav (871 kB) демонстрирует восстановление исходного речевого сообщения. Обратим внимание, что коррекция не является абсолютной – соотношение сигнал/шум несколько ухудшилось относительно качества исходного сигнала, что обусловлено характеристиками квантователя (при записи использовалась примитивная оцифровка с помощью стандартной звуковой карты). Этот эффект еще более наглядно проявляется при коррекции сбоев, следующих через каждый пятый байт – файл restore5_iter1.wav (871kB) (зашумленный файл не прилагается, там ничего невозможно услышать кроме шума). Тем не менее повторная коррекция (файл restore5_iter2.wav (871 kB)) позволяет улучшить соотношение сигнал/шум до приемлемых величин. Т.е. требуемая точность коррекции является функцией вычислительной сложности примененного алгоритма.

 

 Достоинствами предлагаемого метода (не алгоритмов – они могут быть любыми) можно считать:

 

 

 Никак не претендуя на завершенность, можно предполагать, что принцип коррекции ошибок на базе априорного знания найдет применение в практических приложениях. Во всяком случае, для передачи электрокардиограммы нам удалось использовать его с ожидаемыми результатами.