Категории публикаций
Публикации - Электрокардиография
Квазиоптимальная цифровая режекторная фильтрация сетевой помехи и ее гармоник
09.06.2010
Крамаренко А.В.
И в это время в полной тишине прозвучала реплика Н. Н. Моисеева, сидевшего в первом ряду зала: «Оптимального в природе ничего нет, разве что миниюбка на максижопе — минимальные затраты при максимальном эффекте». Зал взорвался хохотом и аплодисментами. http://scilib.narod.ru/Avia/Samoilovich/index.html
Действительно, в природе нет ничего оптимального. И методы фильтрации сетевой помехи в приборах медицинского назначения тому подтверждение.
Попробуем сформулировать требования к идеализированной системе подавления сетевой помехи. При этом будем учитывать не только достигнутые характеристики, но и простоту или, наоборот, сложность реализации, трудозатраты на разработку, а также влияние системы на себестоимость прибора.
В качестве важнейшего требования будем предполагать необходимость фильтрации всех, в том числе и четных, гармоник сетевой помехи. Причина очевидна и заключается в том, что по мере роста количества импульсных бестрансформаторных блоков питания бытовых потребителей возрастает величина помех на частотах гармоник электрической сети. В качестве экспериментального подтверждения можно привести следующую иллюстрацию:
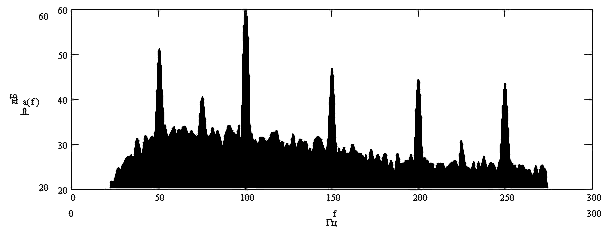
Рис.1 Типичный спектр шума офисного помещения.
Очевидно, что для получения качественного сигнала в диапазоне 0-200Гц фильтрация помехи 100Гц имеет на 10дБ большее значение, а помехи 150 Гц – приблизительно такое же, как и собственно сетевой помехи. Кроме того, помехи на частотах 200, 250, 300 Гц также будут вносить некоторый вклад суммарную помеху на зарегистрированной электрокардиограмме, электроэнцефалограмме и т.п.
Т.е. не вызывает сомнений, что оптимальный фильтр сетевой помехи должен иметь гребенчатую АЧХ с минимумами на частотах, кратных 50, и с подавлением в точках минимумов не менее 40 дБ. При этом он должен обеспечивать линейную ФЧХ, иметь регулируемую полосу режекции и перестройку по частоте при необходимости, не допускать «звона» после высоковольтной импульсной помехи, ни в каком случае не менять ни амплитуду, ни форму полезного сигнала при включении/выключении.
Существующие в современных медицинских приборах фильтры не являются оптимальными т.к. у каждого имеются свои недостатки.
В то же время, реализация требований к подобному оптимальному фильтру, на первый взгляд, полностью исключает возможность его простой реализации, т.е. воображение сразу предлагает весьма сложную комбинацию различных фильтров.
Дьявол, однако, как всегда скрывается в деталях. И одной из них можно считать требование фильтра, ограничивающего полосу частот снизу. Поясним: для сигналов ЭКГ, ЭЭГ и т.п. необходимо исключить постоянную составляющую сигнала. При этом обычно используется два фильтра – аналоговый непосредственно в приборе с постоянной времени много больше требуемой, и второй – цифровой, который ограничивает полосу на требуемой величине: 3.2 или 2.3 сек для ЭКГ, 0.05, 0.1, 0.3, 0.7 сек для ЭЭГ.
Справка: в медицине полоса снизу традиционно определяется не в герцах, а в секундах, т.е. в величине времени, которая необходима для того, чтобы поданный на вход сигнал 1.0 принял значение 1/е на выходе. При этом очень желательно, чтобы фильтр давал экспоненциальный спад во временной области, т.е. максимально точно имитировал работу RC цепи, которая использовалась в приборах для этой цели ранее. Это далеко не глупое требование, т.к. неправильно спроектированный фильтр может иметь постоянную времени 3.2 секунды, например. Но кривая, сильно отличающаяся от экспоненты, приведет к тому, что сигнал ЭКГ будет искажен, особенно в сегменте ST. И это действительно наблюдается у некоторых электрокардиографов и вызывает справедливое раздражение у врачей: по метрологии у прибора все «ОК», а есть у больного ишемия или нет, непонятно.
Используем простейший рекурсивный фильтр вида:

(здесь и далее для удобства гг. программистов фильтры представляются сразу в программном коде без представления в традиционной форме, которая обычно не востребована читателями).
Этот фильтр дает хорошее приближение к требуемой экспоненте во временной области, прост в реализации, не требует никаких по существу ресурсов, не искажает сигнал и легко управляется. Экспериментальная выходная кривая после подачи на вход сигнала Хевисайда представлена на Рис.2.
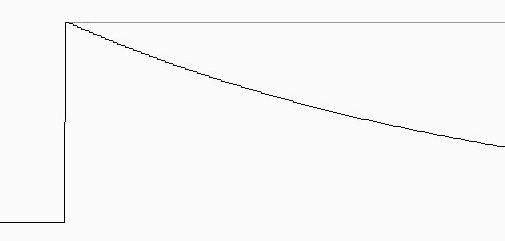
Рис.2 Рекурсивный фильтр устраняет постоянную составляющую сигнала по закону, весьма близкому к характеристикам общепринятой RC цепи.
Характеристики в частотной области представлены на Рис.3.
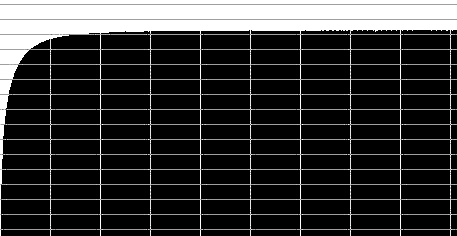
Рис.3 Сетка проведена через 3дБ по оси Y и через 2Гц по оси X.
Но т.к. аппетит приходит во время еды, было бы очень недурно сделать подобную характеристику симметричной и гребенчатой Рис.4.
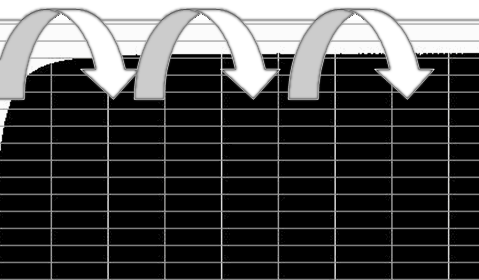
Рис.4 Для фильтрации сетевой помехи и ее гармоник необходима гребенчатая характеристика фильтра.
Как ни странно, но эта задача легко реализуется распараллеливанием базового фильтра в группу, где число фильтров равно отношению частоты дискретизации к частоте основной гармоники помехи. В том случае, когда эти частоты делятся нацело (т.е. можно использовать фильтрующие свойства доли частоты дискретизации), появляется возможность построить универсальный фильтр, гребенка которого закрывает все гармоники помехи. При этом требуется лишь пропорционально уменьшить делитель для сохранения базовой постоянной времени.
Экспериментальная характеристика фильтра в частотной области представлена на Рис.5
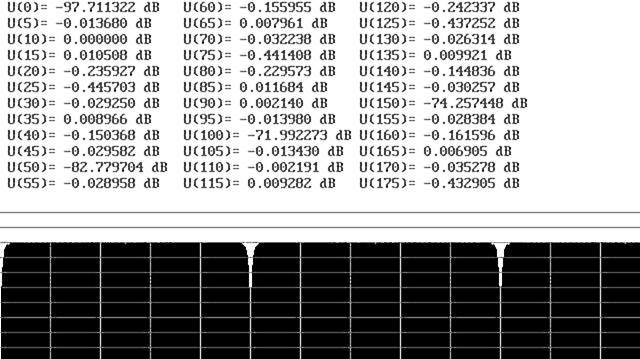
Рис. 5 Характеристика квазиоптимального фильтра (применительно для сигнала ЭЭГ). Сетка проведена через 3 дБ по оси Y и через 10 Гц по оси X. Обратите внимание на неравномерность в полосе пропускания вне полос режекции.
Программная реализация может быть выполнена следующим образом:
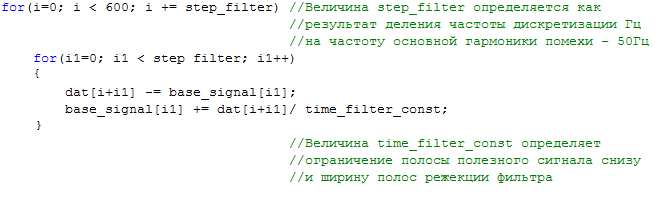
Очевидно, что в данном случае изменения заключаются лишь в том, что base_signal стал массивом, в который записывается не постоянная составляющая, а полный период помехи вместе с величиной постоянной составляющей. Понятно, что в данном случае фильтруется не только синусоидальная составляющая основной гармоники помехи, но и любые ее гармоники. Т.е. если помеха представляет собой меандр, например, или любое другой сколь угодно сложный сигнал, то все его составляющие, кратные периоду основной гармоники, будут вычитаться из полезного сигнала. Что и требовалось.
Разумеется, фильтр легко управляется. Изменения параметра time_filter_const представлены на следующих рисунках:

Рис. 6. Различные варианты характеристик одного и того же фильтра.
Во временной области данный фильтр ведет себя следующим образом: при появлении сигнала помехи, совпадающего по частоте с любой из полос режекции, наступает период, в течение которого помеха снижается по амплитуде и компенсируется.
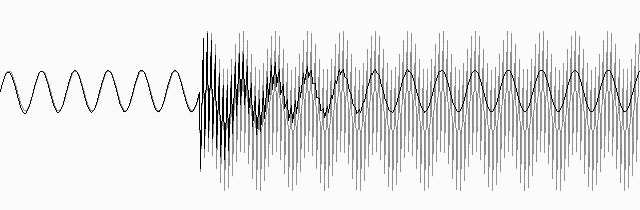
Рис.7 Компенсация возникшей помехи: серым цветом показан исходный сигнал, черным – отфильтрованный. Обратите внимание на полное отсутствие фазовых задержек и изменений амплитуды полезного сигнала.
Разумеется, фильтр работает также и по ограничению полосы пропускания снизу:
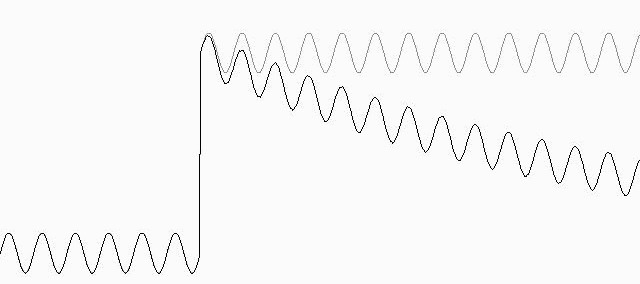
Рис. 8. Компенсация внезапно возникшей постоянной составляющей сигнала. Типичная ситуация «успокоителя» сигнала ЭКГ – в данном случае достаточно кратковременно уменьшить постоянную времени для того, чтобы не только скомпенсировать постоянную составляющую «разрядить конденсатор», но и быстро адаптироваться к изменившейся амплитуде помехи.
Может быть интересным анализ отклика системы на единичный выброс в отсчетах АЦП. Очевидно, что эффект «звона» фильтра присутствует, однако, в отличие от классических фильтров, звон представляет собой не помеху 50Гц, а короткие импульсы, следующие с частотой 50Гц. Естественно, что последующая цифровая фильтрация может устранить их со значительно большим коэффициентом подавления. В случае применения медианной, например, фильтрации (при некоторой избыточности частоты дискретизации), эффект «звона» фильтра будет устранен полностью.
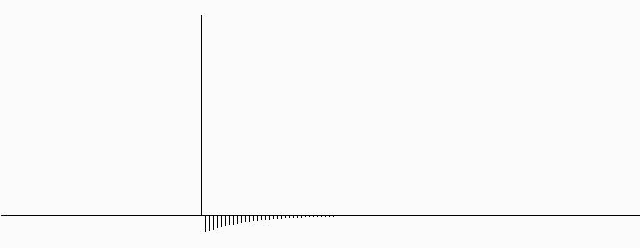
Рис.9. Отклик фильтра на единичный высоковольтный импульс.
Разумеется, фильтрацию сетевой помехи и ее гармоник можно вести и КИХ фильтрами, использующими фильтрующие свойства доли частоты дискретизации. Но, в полном соответствии с теорией, падение добротности при идентичных порядках и неизбежное запаздывание на величину длительности окна, не дают возможности достигнуть таких же результатов.
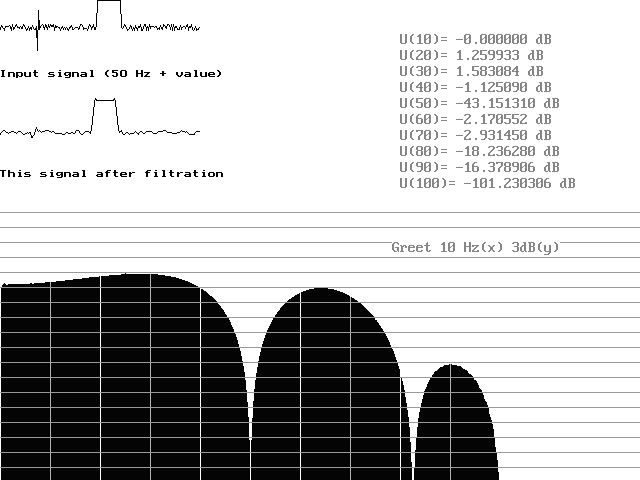
Рис.10. Решение той же задачи с помощью нехэмминговского КИХ фильтра.
Но ничего оптимального, как уже было указано, в природе нет, поэтому предлагаемое решение можно, на мой взгляд, считать близким к требуемому, т.е. квазиоптимальным. В качестве рекомендаций по использованию данного фильтра необходимо указать следующее: этот фильтр должен быть первым после АЦП, а уже следом за ним – фильтры, ограничивающие полосу сверху.
Причина в том, что у предлагаемой реализации режекторного фильтра есть не только достоинства, но и один недостаток. Заключается он в том, что частота «разряда конденсатора» не может быть выше 50Гц и на пологих скатах (см. Рис.2) визуально заметна некоторая «ступенька» на кривой. В случае последующей фильтрации она исчезает.
Кроме того, не следует стремиться к избыточному (сверх необходимого) увеличению параметра time_filter_const т.к. частота сети переменного тока тоже имеет некоторый допуск, обычно в пределах 0.1Гц.
Дополнение от 23.08.2010. Автор дополнения - Крамаренко Ю.А.
Для проверки изложенного в статье способа фильтрации была написана программа, которая выполняет обработку аудио файлов формата wav(PCM).
Исходный код на языке С, описание и исполняемый файл можно скачать по этой ссылке.
Ниже приведены результаты обработки двух аудио файлов.
1
К исходному фрагменту музыкальной композиции sample1_original.wav был добавлен прямоугольный сигнал с частотой 50 Гц и скважностью 50%. Получившийся файл sample1_50hz.wav был обработан программой с параметром time_filter_const равным 2.0. Результат: sample1_processed.wav.
Как можно убедиться, помеха полностью удалена.
2
В следующем фрагменте sample2_200hz.wav для иллюстрации адаптивности фильтра помеха с частотой 200 Гц периодически добавляется к исходному сигналу. В результате фильтрации sample2_processed.wav в моменты включения помехи можно наблюдать быстро затухающий прямоугольный сигнал с частотой 200 Гц.
Таким образом на примерах была проиллюстрирована работа фильтра.
Дополнение от 18.10.2010.
Для использования в холтеровской электрокардиографии описанный фильтр не слишком пригоден. Причина заключается в том, что реальные помехи с частотой осветительной сети модулированы по амплитуде при смещении пациента относительно источника помех (особенно это относится к случаям длительного мониторинга, когда пациент свободно двигается). Пики на гребенке спектра у таких помех значительно шире (в общем случае – более чем вдвое относительно частоты модуляции) чем у сигнала с частотой осветительной сети. И для решения такой задачи необходимо расширить полосы заграждения при неизменной постоянной времени, т.е. ограничении полосы пропускания снизу. Амплитудно-частотная характеристика фильтра должна выглядеть следующим образом.

Рис.11. Пригодная для использования в электрокардиографии АЧХ фильтра.
Поставленная задача достигается применением фильтра вида (приводится программная реализация для частоты дискретизации 400 Герц).
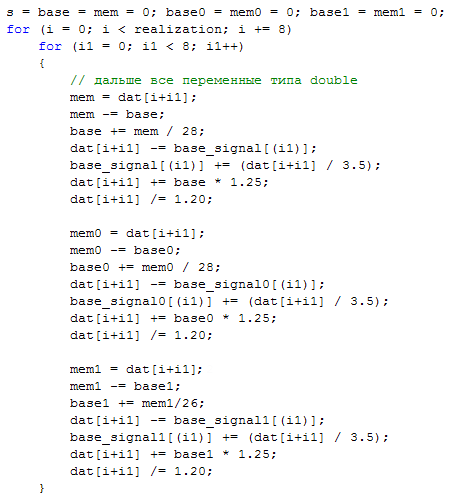
При необходимости дополнительного ограничения полосы пропускания «сверху» т.е. введения «антимускульного» фильтра целесообразно использовать обычный КИХ фильтр с коэффициентами: 0,03516; -0,10355; -0,11811; 0; 0,2645; 0,6035; 0,8887; 1; 0,8887; 0,6035; 0,2645; 0; -0,11811; -0,10355; 0,03516; (содержимое массива wind1).
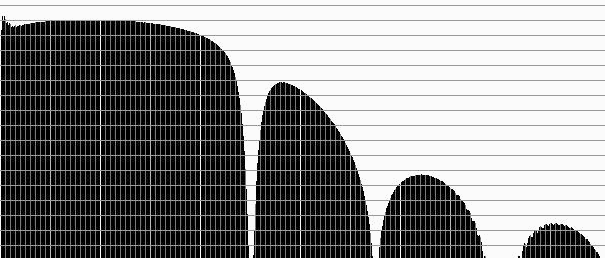
Рис.12. Дополнение «антимускульным» фильтром
Программная реализация (опять же – для частоты 400 Герц)

Понятно, что для адаптации к быстро меняющимся уровням помехи фильтр должен обеспечивать максимально быстрое подавление вновь появившихся (либо изменившихся по амплитуде) помех. Иллюстрации его работы (во временной области) представлены на следующих рисунках.

Рис.13. Подавление вновь появившейся нарастающей по амплитуде помехи.

Рис.14. То же для 100% модулированной помехи с периодом модуляции менее 1 сек.
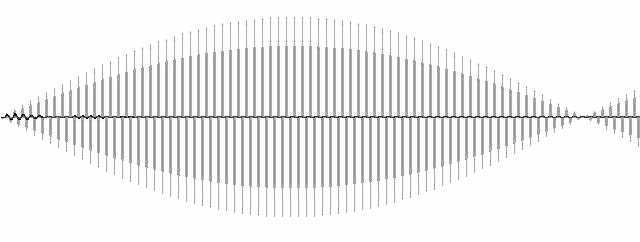
Рис.15. Подавление помехи при амплитудной перемодуляции.

Рис.16. То же для перемодуляции с высокой частотой модулирующего сигнала. Наблюдается неполное подавление помехи.
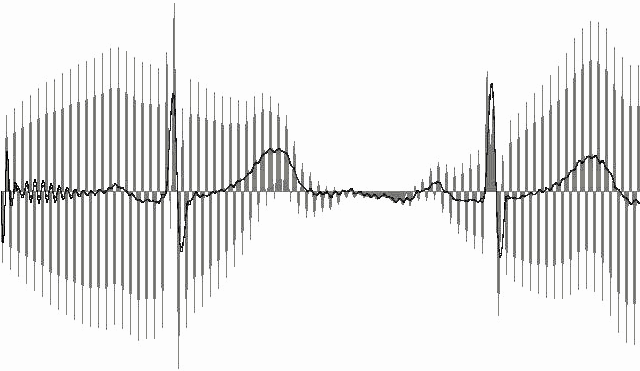
Рис.17. Подавление помехи в искусственно созданной аддитивной смеси «чистого» ЭКГ сигнала и амплитудно-модулированной сетевой помехи.
Любая фильтрация вносит искажения в сигнал, что видно из следующей иллюстрации.
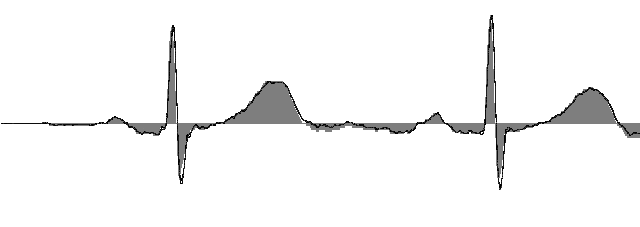
Рис.18. Выделенный сигнал ЭКГ (серым сплошным – исходный, линиями – результат с «антимускульным» фильтром и без него). Хорошо видно фазовое запаздывание как результат фильтрации.
Рассмотрим случай подавления реальной помехи для холтеровского ЭКГ сигнала.
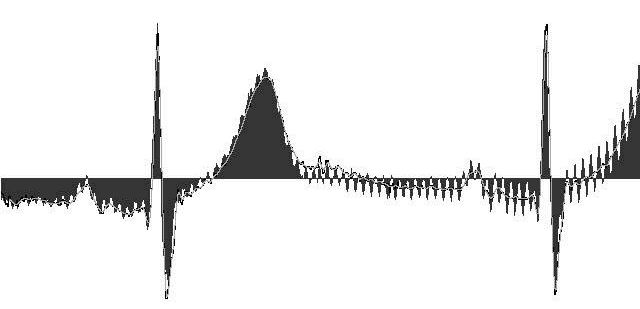
Рис.19. Фильтрация помехи 50 Герц. Серым цветом показан исходный сигнал, линиями результат фильтрации с «антимускульным» фильтром и без него.
Очевидно, что результат в данном случае далек от желаемого. Фильтрованная ЭКГ содержит как шумовые компоненты, не устраненные даже «антимускульным» фильтром, так и «просачивание» помехи (участок показан стрелкой).
Попробуем выяснить причину. Вычислим разность между исходным сигналом и результатом фильтрации.
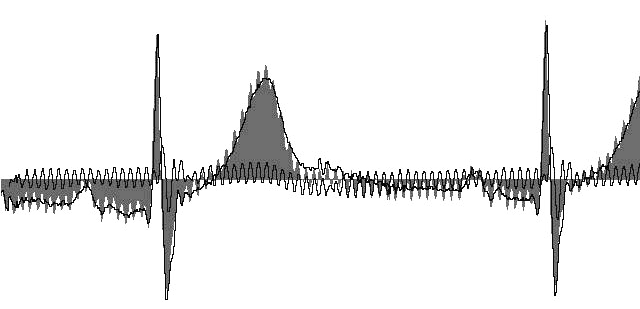
Рис.20. Разностный сигнал соответствует помехе с частотой осветительной сети.
Выделенная помеха практически не модулирована по амплитуде.
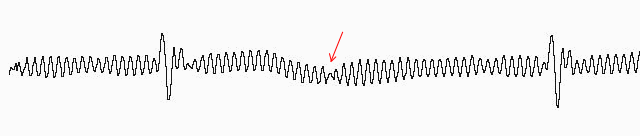
Рис.21. Однако место, отмеченное стрелкой, показывает, вероятно, момент смены фазы помехи.
Проверим эту гипотезу и подадим сигнал на фазовый детектор.

Рис.22. Сигнал после ФД. Хорошо виден момент смены фазы помехи.
Т.е. в данном случае имеется самый, пожалуй, неприятный случай помехи. Причем невозможно определить, фазовая модуляция имела место вследствие изменения фазы помехи, либо вследствие возникшей задержки импульсов дискретизации. К слову сказать, опрос АЦП средствами ОС Windows может давать спонтанные смещения опросов на величину до 10 миллисекунд вследствие многозадачности режима (проверено экспериментально для «XP»). В то же время, возникновение «чистой» угловой модуляции сетевой помехи при использовании системы ЭКГ отведений, дающей классическую «восьмерку» диаграммы направленности антенны, практически невозможно, т.к. смена фазы помехи будет происходить вследствие АМ перемодуляции, а не изолированной ФМ. Продемонстрируем важность спектральной чистоты гетеродина и недопустимость джиттера при дискретизации (что, в общем-то, является общим местом в проектировании радиотехнических систем).
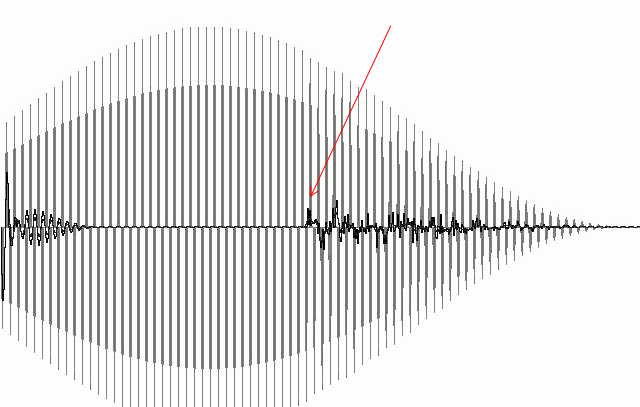
Рис. 23. Стрелкой показан момент возникновения джиттера дискретизирующей последовательности. Хорошо виден перенос энергии помехи в псевдошумовую последовательность, которая никак не устраняется режекторным фильтром.
Вывод: никакая фильтрация не поможет в том случае, если хотя бы один из компонентов системы функционирует нерасчетно.
Категории:
- Войдите, чтобы оставлять комментарии
Адрес: Украина, 61057, Харьков, а/я 39,
тел./факс.: +38(050)0113940, +38(057)7290409.
E-mail: tredex@tredex-company.com
tredex.office@gmail.com