Категории публикаций
Публикации - Электрокардиография
Свёрточно-корреляционный алгоритм выделения QRS комплекса
08.10.2011
А.В. Крамаренко, Ю.А. Крамаренко
Если кажется, что работу сделать легко, это непременно будет трудно. Если задача трудна даже на вид, значит, решить ее абсолютно невозможно.
(Теорема Стакмайера)
(Теорема Стакмайера)
В настоящее время для решения задачи обнаружения сердечного сокращения по сигналу электрокардиограммы практически повсеместно используется алгоритм Pan J. , Tompkins, “A real time QRS detection algorithm”, IEEE Trans. Biomed. Eng., vol. BME-32, pp. 230-236, 1985.
Он вполне соответствует требованиям и обеспечивает (по оптимистическим оценкам) корректное детектирование не менее 95% комплексов. Тем не менее, с учетом возросших вычислительных мощностей современных процессоров, все чаще предлагаются новые алгоритмы (нейронные сети, волновое преобразование, частотно-временные алгоритмы и различные варианты «улучшенного» базового алгоритма), которые должны по замыслу разработчиков повысить точность детектирования. Но неизбежной платой становится значительный рост вычислительной сложности при неочевидных выигрышах в точности выделения QRS комплекса.
Многолетний опыт использования обычных и холтеровских ЭКГ систем показал: задача детектирования QRS достаточно нетривиальна и намного более сложна, чем, допустим, обнаружение импульса известной формы в аддитивной смеси с белым гауссовским шумом. ([1])
Рассмотрим входные условия более тщательно, чем это обычно делается при постановке задачи на изготовление программного обеспечения для QRS детектора. Сразу отметим, что искомый комплекс представляет собой довольно изменчивую структуру, более того, в него включены, по меньшей мере, два класса:
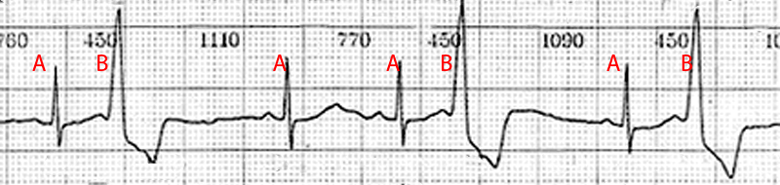
- QRS для нормального внутрисердечного проведения
- QRS для аномального сокращения, т.н. «широкий комплекс», характерный для желудочковых экстрасистол, различных блокад ветвей пучка Гиса и других патологий.

Рис.1. Обычный (А) и «широкий» (В) QRS комплексы
Это условие очень важно учитывать при разработке алгоритма т.к. амплитудно-временные и спектральные характеристики обоих комплексов отличаются весьма значительно. Понятно, что с помощью универсального решающего правила не удастся обеспечить как равную эффективность детектирования их, так и низкие вероятности ошибок. И только применение оптимального приёмника Котельникова может быть действительно хорошим выбором для решения поставленной задачи. ([2])
Что же касается помеховой обстановки, в которой производится обнаружение/распознавание QRS, то она представляет собой очень сложную смесь аддитивных шумов, аддитивных и мультипликативных - обусловленных дефектами электродов - компонентов, систематических узкополосных помех в виде «фона» переменного тока и артефактов движения (включающих в себя кроме собственно мышечных компонентов также и импульсные низкочастотные помехи).
Что же касается помеховой обстановки, в которой производится обнаружение/распознавание QRS, то она представляет собой очень сложную смесь аддитивных шумов, аддитивных и мультипликативных - обусловленных дефектами электродов - компонентов, систематических узкополосных помех в виде «фона» переменного тока и артефактов движения (включающих в себя кроме собственно мышечных компонентов также и импульсные низкочастотные помехи).
Начнем с шумов и двигательных артефактов. Спектр этих помех существенно отличается от спектра белого шума и, скорее, близок к спектру фликкер-шумов (1/f).
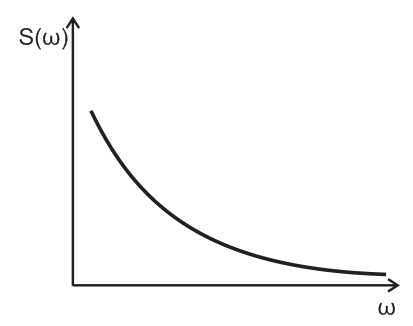

Рис.2. Типичный спектр фликкер-шума.
Спектр единичных выбросов сигнала иногда может быть вообще неотличим от спектра QRS комплекса в полосе пропускания согласованного фильтра. Т.е. первая ловушка подстерегает разработчика именно здесь: согласованная фильтрация не дает желаемого результата просто потому, что импульсная помеха может иметь амплитуду много больше искомого сигнала и просачивание её через периферию полосы пропускания согласованного фильтра может давать отклик, сравнимый по уровню с откликом от обнаруживаемого сигнала.
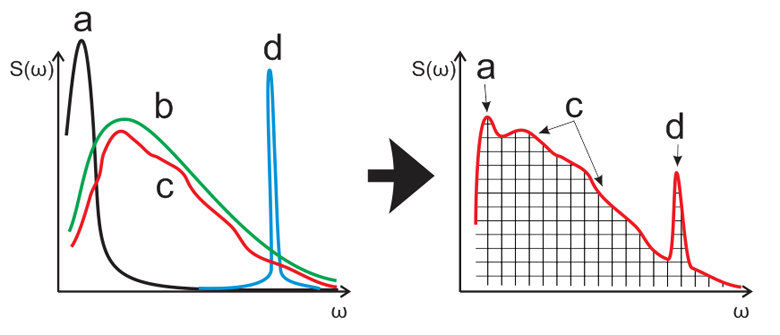

Рис. 3. Просачивание высокоамплитудных низкочастотной (a) и помехи сети переменного тока (d) через периферию полосы пропускания согласованного со спектром QRS комплекса (c) фильтра (b). Обратите внимание на пики (a) и (d) на правом графике.
Разумеется, отбеливание шума ещё менее удачный вариант решения задачи, что совершенно справедливо учтено Паном и Томкинсом в их базовом алгоритме. Наиболее эффективным в этом случае будет фильтр с максимальным коэффициентом прямоугольности, особенно большое значение имеет подавление низкочастотных компонентов.
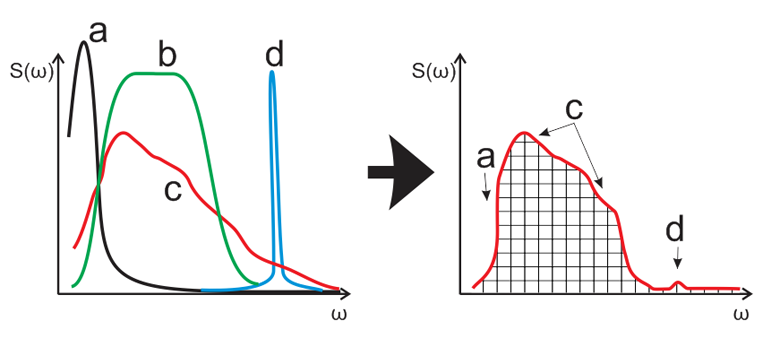

Рис. 4. Подавление высокоамплитудных низкочастотной (a) и помехи сети переменного тока (d) при использовании полосы пропускания максимально «прямоугольного» полосового фильтра (b). Обратите внимание, что пики (a) и (d) на правом графике практически подавлены. В результате соотношение сигнал/помеха лучше, чем в предыдущем случае (Рис.3).
Что касается систематических узкополосных помех в виде фона переменного тока, то в современных электрокардиографах эта задача в большинстве случаев решена хорошо. Если же требуется дополнительная фильтрация гармоник сетевой помехи, то можно предложить решение, описанное в [3].
Рассматривая задачу чуть шире и пытаясь найти аналогии в области обработки сигналов, легко увидеть, что задача обнаружения QRS совсем не похожа на классическое обнаружение известного сигнала в смеси сигнал/шум. Она ближе к задаче обнаружения сигнала с приблизительно известными характеристиками на фоне преднамеренных как шумовых, так и активных имитационных помех, и решать ее нужно примерно так же, как это делается в военной технике. Кроме того, следует учитывать, что живой оператор физически не в состоянии оценивать корректность принятого решения по каждому обнаруживаемому комплексу. Поэтому алгоритм обнаружения/распознавания должен включать в себя функцию «идеального наблюдателя», когда решение «это искомый QRS»/ «Это не QRS, а похожая на него импульсная помеха» принимается автоматом.
Попробуем обосновать выбор решений в близком к теоретическому оптимуму алгоритме обнаружения QRS.
- Ограничение полосы пропускания фильтром с максимальным коэффициентом прямоугольности и полосой, достаточной для вписывания Фурье-образа сигнала. Несмотря на некоторую энергетическую неоптимальность такой фильтрации, она обеспечивает максимальную страховку от высокоамплитудной внеполосной импульсной помехи. Т.е. суммарный баланс цены ошибки получается заведомо положительным.
- Свертка сигнала с его прототипом, с учетом, разумеется, того, что сигнал будет изменен предшествующей фильтрацией. Т.е. прототип должен соответствовать уже фильтрованному сигналу. Энергетический оптимум такого решения не нуждается в обоснованиях – это аксиома радиотехники.
- Т.к. исходный сигнал известен только приблизительно, в качестве прототипа сначала должен использоваться усредненный образ фильтрованного QRS комплекса популяции, а затем, по мере накопления наблюдений в анализируемой электрокардиограмме, он должен адаптивно заменяться прототипом, характерным для данного пациента. Конечно, чтобы обеспечить возможность последующего выбора, свертка должна производиться как с прототипом нормального сердечного сокращения, так и аномального, т.е. «широкого» комплекса.
-
Отклик системы после свертки представляет собой новый сигнал, который должен быть оценен по степени достоверности обнаруженного феномена. И здесь разработчика подстерегает другой «подводный камень», заключающийся в том, что сигнал ЭКГ весьма вариабелен по амплитудным характеристикам. Т.е. амплитуда двух последующих откликов системы на два сердечных сокращения может отличаться на порядок. И это при условии, что ни один из этих откликов не относится к числу артефактов – оба нужно квалифицировать как сердечные сокращения
 Рис.5. В данном случае имеются очень различные QRS двух последующих сердечных сокращений.
Рис.5. В данном случае имеются очень различные QRS двух последующих сердечных сокращений. - Понятно, что с учетом такой амплитудной вариабельности сигнала любые амплитудно-пороговые методы будут по определению давать высокую вероятность ошибки. Поэтому необходима высокоэффективная адаптивная система автоматической регулировки усиления. При этом вероятности ошибок первого/второго рода будут обусловлены практически полностью качеством работы системы АРУ.
- Т.к. «абсолютных» систем АРУ в природе не бывает, целесообразно вместо нее использовать метод, предложенный в [4] , когда решение принимается не пороговыми обнаружителями, а пирсоновским коррелятором, сравнивающим полученный после оптимальной фильтрации отклик с прототипом этого отклика. Т.е. на выходе всей системы вычисляется величина степени подобия принятого феномена прототипам, которые записаны в памяти. Причем эта величина нормирована в величинах -1,0…1,0. Т.к. прототипов не один (в нашей постановке задачи их два – для нормального и «широкого» комплекса), то реализация оптимального приёмника Котельникова обеспечивается простым выбором отклика, имеющего большую степень подобия (при условии, что он превышает установленный для выбора сигнал/артефакт порог пирсоновской корреляции).
- Третий «подводный камень» ждет нас во врачебных критериях: по существующим канонам даже безупречный (с R=1,0) QRS с амплитудным значением менее -20дБ и более +20дБ уже не есть признак сердечного сокращения, а весьма вероятный артефакт. Это необходимое условие перекодировки решений на язык оператора. Поэтому излишне высокоамплитудные комплексы должны иметь пониженный коэффициент корреляции, равно как и низкоамплитудные. Т.к. в рамках пирсоновского коррелятора это сделать невозможно, необходимо вводить предыскажения во входной сигнал и использовать нелинейную перекодировочную кривую.

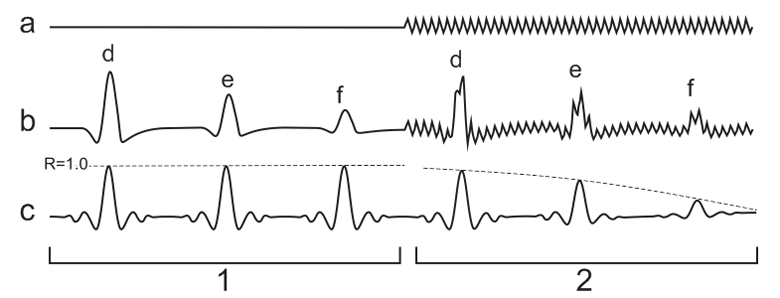
Рис. 6. Аддитивный сигнал «гребенки» - (а), входной послесвёрточный сигнал – (в), убывающие по амплитуде комплексы – (d, e, f), выходной пирсоновский сигнал – (с). Для случая 1 имеем равную величину отклика, для случая 2 его уровень прогрессивно понижается по мере снижения уровня входного сигнала.

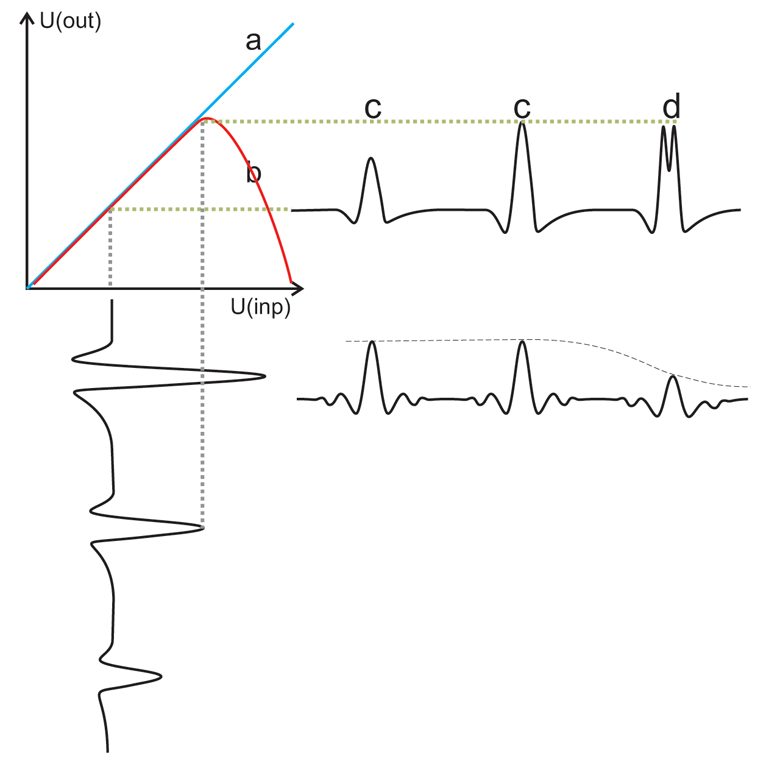
Рис.7. Линейная (а) и нелинейная (в) перекодировочные таблицы, неискаженный (с) и искаженный (d) послесвёрточные комплексы. Снижение уровня выходного сигнала пирсоновского коррелятора.
В результате получается близкий к оптимуму (в реальной помеховой обстановке) алгоритм приема. Предельно упрощая, его работу можно описать так: cкользящее окно в реальном времени сдвигается по фильтрованному сигналу ЭКГ. Непрерывно выполняя свертку входного сигнала с двумя QRS-прототипами и вычисляя пирсоновскую корреляцию с послесвёрточными прототипами, можно с константным запаздыванием для каждого дискретного отсчета сигнала электрокардиограммы получить апостериорную вероятность обнаружения искомых QRS комплексов (нормального и «широкого»). И если разрешенный порог корреляции превышен, то в соответствии с критерием Котельникова обеспечивается решение: обнаружен или нет QRS, а если он обнаружен, то какой именно. При этом для каждого обнаруженного комплекса имеется также апостериорная вероятность ошибки решения, что становится входным сигналом для адаптивной системы, подстраивающей работу алгоритма для сигнала ЭКГ данного пациента.
Учитывая то, что все современные системы ЭКГ многоканальны, в отдельный вопрос следует выделить совмещение результатов внутриканальных корреляций с целью принятия консолидированного решения. Т.к. в наиболее общем случае (с целью минимизации риска ошибки) мы должны полагать, что синхронная регистрация ЭКГ идет в ортогональных каналах, то единственным решением может быть только гипотенуза в пространстве, мерность которого определена количеством каналов, т.е.
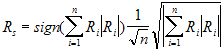
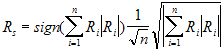
где
n – количество каналов,
Ri - коэффициент корреляции в канале i,
Rs - результирующий коэффициент корреляции.
n – количество каналов,
Ri - коэффициент корреляции в канале i,
Rs - результирующий коэффициент корреляции.
Что касается вычислительных затрат, то для 3-х канальной ЭКГ с частотой дискретизации 400Гц при обработке в реальном времени, они составили 0.17% загрузки процессора (AMD Turion II P520 (2.3 ГГц), ОС Windows 7, 3 ГБ ОЗУ, программа на языке С++ без использования многопоточности).
Очевидно, что описанный алгоритм должен обеспечить корректное детектирование QRS комплексов в тех случаях, когда решение этой задачи никакими другими способами невозможно. Попробуем подтвердить это утверждение экспериментально. Используем холтеровскую запись, сделанную на старом американском приборе. Частота дискретизации 128 Гц, недостаточный динамический диапазон, линейная передискретизация к частоте 400Гц, достаточная степень зашумленности, имеются двигательные и электродные артефакты, которые хорошо имитируют QRS комплексы.
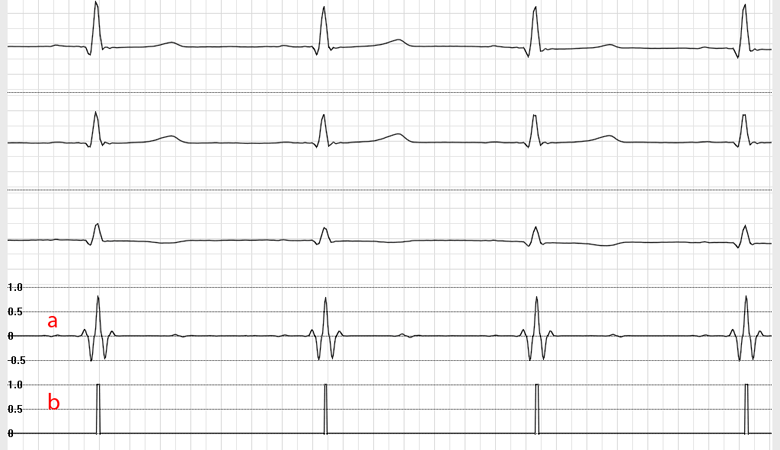
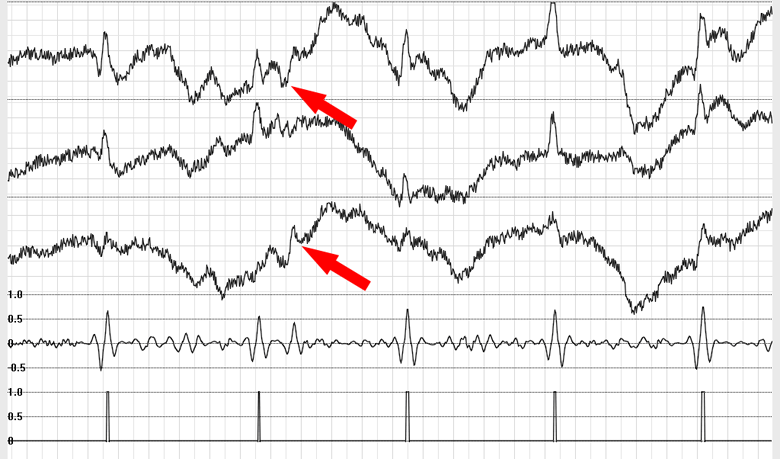
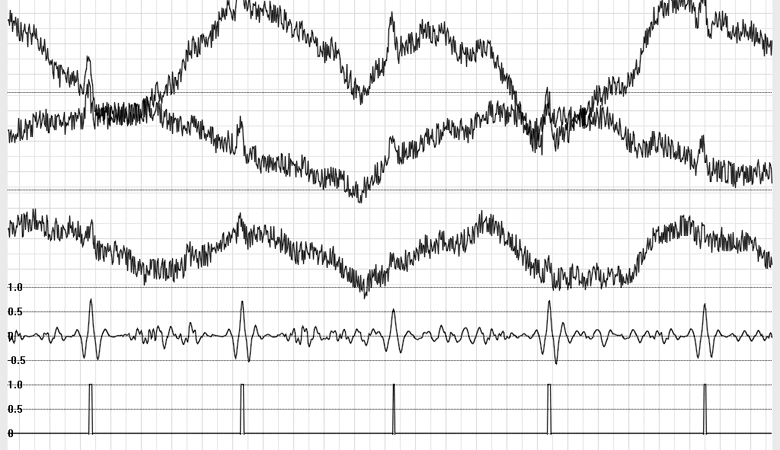
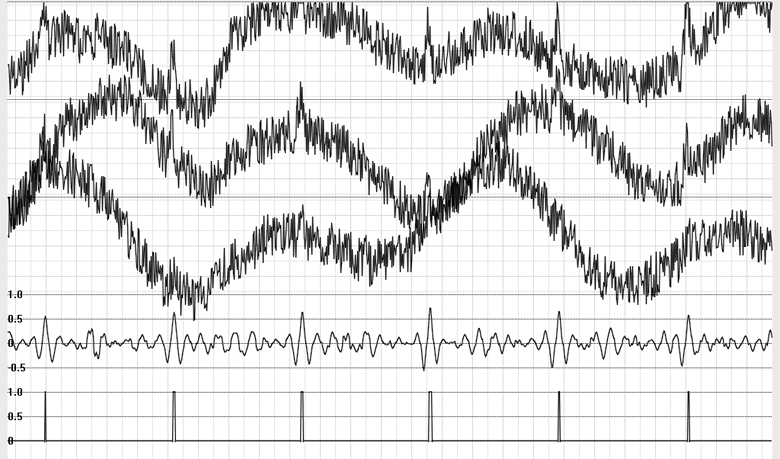
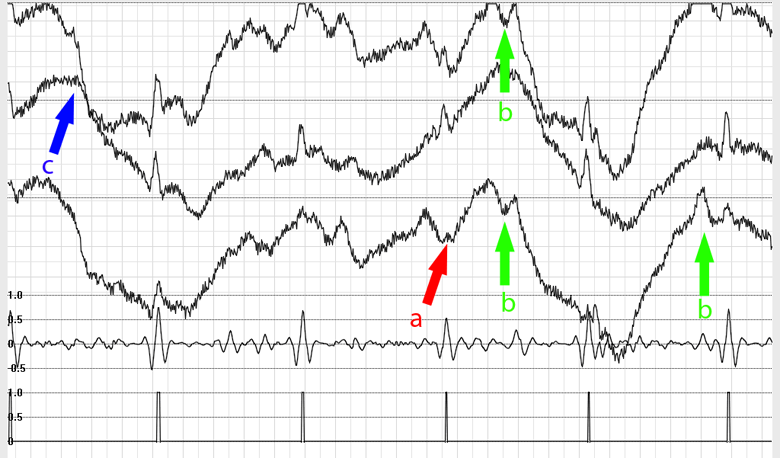

Рис. 8. Фрагмент безартефактной холтеровской записи. Кривая а – выходной пирсоновский корреляционный коэффициент, кривая b – результат принятия решения, т.е. обнаружение QRS комплекса.

Рис. 9. Фрагмент записи с выраженными трендами, шумом и двигательными артефактами. Имитационная помеха естественного происхождения (отмечена стрелками). Детектор QRS комплекса работает корректно.

Рис. 10. Дополнительно добавлен аддитивный шум равномерного распределения. Корректная работа детектора.

Рис. 11. Дальнейшее повышение уровня шума, дополнительно добавлен низкочастотный сигнал, обеспечивающий тренды с выходом за пределы динамического диапазона аппаратуры. По-прежнему корректная работа детектора.

Рис. 12. Наиболее сложный для анализа фрагмент записи. Стрелкой (а) отмечено место практически полного исчезновения QRS. Визуальное детектирование затруднено. Тем не менее, используемый алгоритм обеспечивает безошибочное обнаружение искомого сигнала как на фоне естественно возникших имитационных помех (b), так и высокоамплитудных низкочастотных артефактов (с).
Выводы: по нашему мнению предлагаемый свёрточно-корреляционный алгоритм обеспечивает близкое к энергетическому оптимуму детектирование QRS комплексов, которое даже теоретически не может быть достигнуто никакими другими способами. Применением пирсоновского коррелятора и исключением блока автоматической регулировки усиления обеспечивается минимизация рисков ошибок первого и второго рода. Реализация принципа Котельникова позволяет перейти к распознаванию комплекса на самом раннем этапе, почти одновременно с обнаружением. Использование системы адаптации прототипов дает возможность через короткое время настроить алгоритм приема для наиболее эффективного детектирования сигнала с учетом индивидуальных особенностей электрокардиограммы пациента. Вычислительная сложность и требования к мощности процессора остаются при этом в допустимых для современной аппаратуры пределах.
Ссылки
Категории:
- Войдите, чтобы оставлять комментарии
Адрес: Украина, 61057, Харьков, а/я 39,
тел./факс.: +38(050)0113940, +38(057)7290409.
E-mail: tredex@tredex-company.com
tredex.office@gmail.com