Publication categories
Publications - Electrocardiography
Convolution-correlation algorithm of QRS complex detection
10/08/2011
Alexander V. Kramarenko, Yuri A. Kramarenko
If it looks easy, it's tough.
If it looks tough, it's damn well impossible.
Stockmayer's theorem, Murphy's laws
If it looks tough, it's damn well impossible.
Stockmayer's theorem, Murphy's laws
At present to solve the problem of cardiac contraction detection by electrocardiogram signal far and wide they use the algorithm Pan J. , Tompkins, “A real time QRS detection algorithm”, IEEE Trans. Biomed. Eng., vol. BME-32, pp. 230-236, 1985.
It quite meets the demand and ensures (optimistically estimated) correct detection of not less than 95 per cent of complexes. Nevertheless, taking into account sky-rocketed computation abilities of contemporary processors, more and more often they propose novel algorithms (neuronal networks, wave transformation, frequency-time algorithms and various versions of "improved" base algorithm, which, according to the developers' conception, increase the accuracy of detection. Alas, the inevitable fee thereat becomes the dramatic growth of computation complexity with unobvious gain in the accuracy of QRS complex detection.
Many years of experience with using ordinary and Holter ECG systems have shown: the problem of QRS detection is rather non-trivial and much more complex than, say, the detection of a pulse with known form in additive mixture with white Gaussian noise. ([1])
Let us consider the input conditions more thoroughly than it is usually done when formulating the task for producing software for a QRS detector. First of all let us note that the complex in question is a rather changeable structure, even more, the one containing at least two classes:
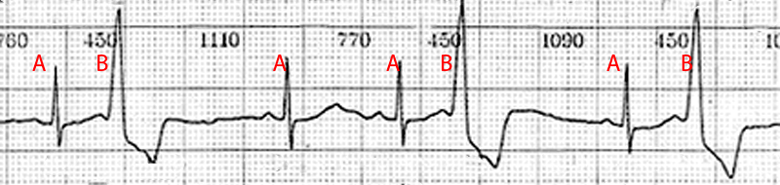
- QRS for normal intracardiac conduction
- QRS for abnormal heart beat, so called "wide complex" characteristic for ventricular premature systoles, various blocks of branches of bundle of His and other pathologies.

Fig.1. Usual (А) and "wide" (В) QRS complexes
It is important to take into consideration this condition when developing the algorithm, as amplitude-temporal and spectral characteristics of both complexes differ quite substantially. It is clear that it is impossible to ensure by means of a universal solving rule both equal efficiency of their detection and low error probabilities. Only the implementation of Kotelnikov's receiver can be a really good choice for solving the problem in question. ([2])
As to the noise environment, in which QRS is detected/recognized, it is a very complex mixture of additive noises. additive and multiplicative, caused by electrode defects, components, systematic narrow-band interference in the form of AC "background" and motion artifacts (including, apart from muscle components themselves, also pulse and low-frequency interference).
As to the noise environment, in which QRS is detected/recognized, it is a very complex mixture of additive noises. additive and multiplicative, caused by electrode defects, components, systematic narrow-band interference in the form of AC "background" and motion artifacts (including, apart from muscle components themselves, also pulse and low-frequency interference).
Let us begin from noise and motion artifacts. The spectrum of this interference differs substantially from the white noise spectrum and rather close to the flicker noise spectrum (1/f).
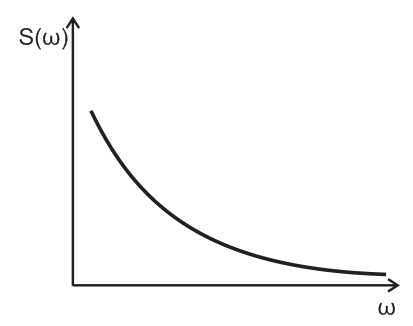

Fig.2. Typical flicker noise spectrum.
Sometimes the spectrum of single signal spikes can be totally undistinguishable from the QRS complex spectrum in the matched filter bandwidth. It is right here lies the first trap in wait for the developer: matched filtering yields no desired result simply because a pulse interference can have an amplitude much higher than the sought signal and its leakage through the bandwidth periphery of a matched filter can give a response compatible as to the level to the response of the signal being detected.
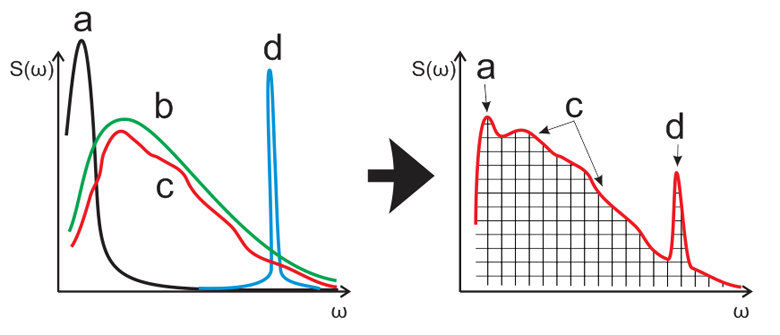

Fig. 3. Leakage of high-amplitude low-frequency (a) and AC mains (d) interferences through the bandwidth periphery of a filter (b) matched with the QRS complex spectrum. Pay attention to peaks (a) and (d) on the right-hand chart.
It goes without saying that whitening the noise is an even worse way to solve the problem, and Pan and Tompkins quite justifiably took this into account in their basic algorithm. The most efficient in this case will be a filter with the maximum coefficient of rectangularity; especially significant is the suppression of low-frequency components.
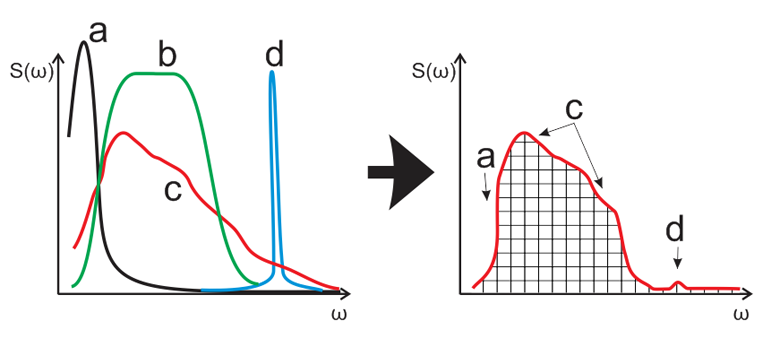

Fig. 4. Suppression of high-amplitude low-frequency (a) and AC mains (d) interferences when using the bandwidth of a maximum "rectangular" band-pass filter (b).Pay attention that peaks (a) and (d) on the right-hand chart are virtually suppressed. As a result the signal-to-noise ratio is better than in the previous case (Fig. 3).
As to systematic narrow-band interference in the form of AC hum, in modern electrocardiographs this problem is solved well in the majority of cases. If an additional filtering of mains interference harmonics is required, we can propose the solution described in [3].
Considering the problem in a wider scope and trying to find analogies in the field of data processing, we can easily see that the problem of QRS detection completely differs from the classical detection of a known signal in a signal/noise mixture. It is closer to the problem of detection of a signal with approximately known characteristics on the background of intentional both noise and active imitation interference and it must be solved approximately in the same way as it is done in military engineering. Besides, we must take into account that a human operator physically cannot estimate the correctness of a made decision on each detected complex. Therefore the detection/recognition algorithm must include the function of an "ideal observer", when the decision "This is QRS sought for"/This is not QRS, but a pulse interference similar to it" is made automatically.
Let us try to motivate the choice of solutions in a close to the theoretical optimum algorithm of QRS detection.
- Limiting the bandwidth by a filter with the maximum coefficient of rectangularity and bandwidth sufficient for inscribing of the Fourier image of the signal. In spite of some power non-optimality of such filtering, it provides maximum insurance against high-amplitude outside-the-band pulse interference. That is the total balance of the error price is a priori positive.
- The signal convolution with its prototype, naturally, taking into account the fact that the signal will be changed by preceding filtering. That is the prototype must correspond to the already filtered signal. The energy optimum of such solution does not require grounding – this is an axiom of radio engineering.
- As the initial signal is known only approximately, first the averaged image of the filtered QRS complex of the population must be used as the prototype, and then, as observations in the electrocardiogram are accumulated, it must be adaptively substituted by a prototype specific for this patient. Of course, the convolution must be made both with the prototype of the normal heart beat and the abnormal one, i.e. "wide" complex.
-
The system response after the convolution is a new signal, which must be evaluated as to the degree of fidelity of the detected phenomenon. And here another hidden reef lies in wait for the developer, the fact that ECG signal is quite variable as to amplitude characteristics. That is the amplitude of two consecutive system responses can differ by an order of magnitude. And this is under the condition that neither of these responses is attributed to artifacts – both must be qualified as heart beats.
 Fig. 5. In this case there are very different QRS of two consecutive heart beats.
Fig. 5. In this case there are very different QRS of two consecutive heart beats. - It is understood that taking into account such amplitude variability of the signal, any amplitude threshold methods will yield by definition a high probability of error. Therefore a highly efficient adaptive system of gain control is required. In this case the probabilities of errors of the first/second kind will be virtually completely determined by the quality of work of the AGC system.
- As "absolute" AGC systems are not encountered in the nature, it is expedient to use in their stead the method proposed in [4], when the decision s made not by threshold detectors, but by Pearson's correlator, which compares the response obtained after optimum filtering with the prototype of this response. That is at the output of the entire system calculated is the degree of similarity of the received phenomenon to prototypes stored in the memory. And this value is normalized in values -1.0… 1.0. As there are more than one prototype (in our statement of the problem there are two – for normal and "wide" complex), the optimal Kotelnikov' receiver is realized by simple choice of the response with the largest degree of similarity (under the condition that it exceeds Pearson's correlation threshold set for the signal/artifact selection).
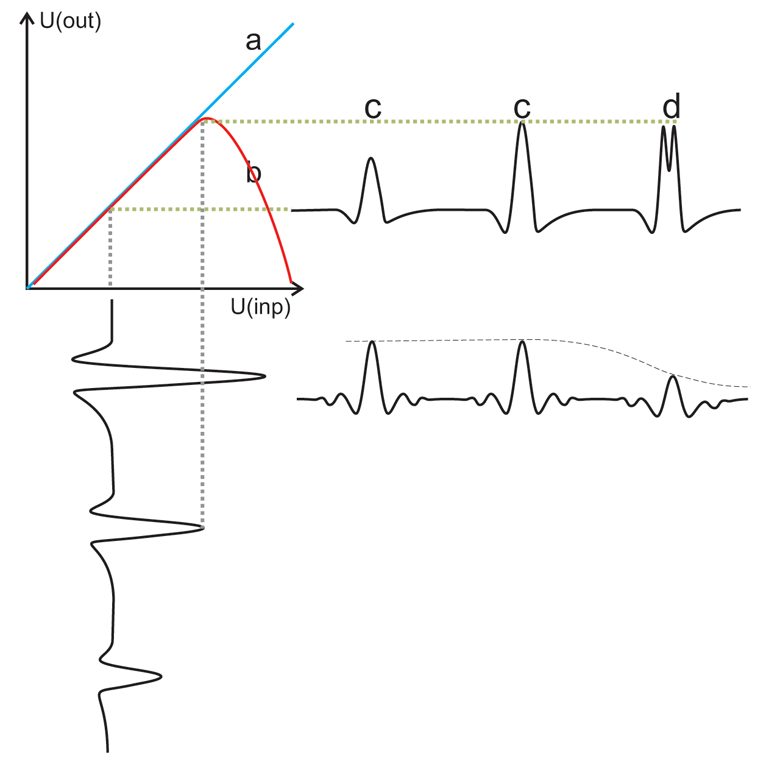
- 7. The "third "hidden reef" waits for us in doctors' criteria: according to the existing canons even the flawless (with R=1,0) QRS with the amplitude value less than -20 dB and greater than +20 dB already is not the sign of heart beat, but rather probable artifact. This is a mandatory condition for solution recoding into the operator's language. Therefore redundantly high-amplitude complexes must have a reduced correlation coefficient, as well as low-amplitude ones. As it is impossible to make this within the framework of Pearson's correlator, it is necessary to introduce predistortions in the input signal and use a non-linear re-encoding curve.

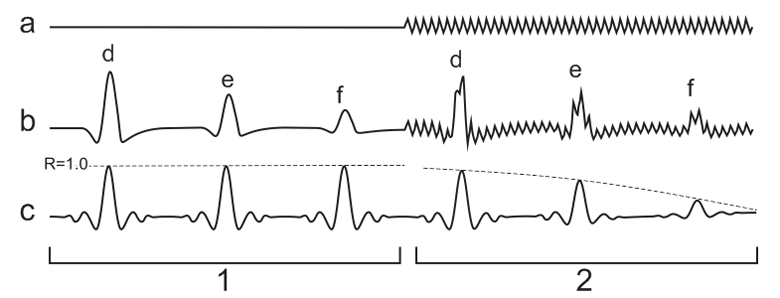
Fig. 6."Comb" additive signal - (а), input afterconvolution signal – (в), complexes decreasing as to amplitude – (d, e, f), output Pearson's signal – (с). For case 1 we have the equal value of the response, for case 2 its value progressively lowers as the input signal level lowers.

Fig.7. Linear (а) and non-linear (в) re-encoding tables, non-distorted (с) and distorted (d) afterconvolution complexes. Lowering of the level of Pearson's correlator output signal.
ВAs a result we obtain a close to the optimum (in a real interference environment) reception algorithm. Simplifying to a limit, we can describe its operation as follows: a sliding window moves in the real time along the filtered ECG signal. Continuously performing the convolution of the input signal with two QRS prototypes and calculating Pearson's correlation with after-convolution prototypes, we can obtain, with a constant delay for each discrete reading of the electrocardiogram signal, the a posteriori probability of detection of QRS complexes sought for (normal and "wide" ones). And if the permitted correlation threshold is exceeded, than, according to Kotelnikov's criterion, a solution is provided: whether QRS is detected or not; and if detected, then namely which. In this case for each detected complex there is also a posteriori probability of solution error, which becomes the input signal for the adaptive system, adjusting the algorithm operation to the ECG signal of a given patient.
Taking into account the fact that all modern ECG systems are multichannel ones, we should outline as a separate question of aligning the intrachannel correlation results in order to make a consolidated decision. As in the most general case (in order to minimize the risk of error) we must suppose that synchronous recording of ECG takes place in orthogonal channels, then the only solution can be the hypotenuse in the space the dimension of which is determined by the number of channels, i.e.
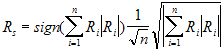
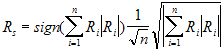
where
n is the number of channels
Ri is the correlation coefficient in channel i
Rs is the resulting correlation coefficient.
n is the number of channels
Ri is the correlation coefficient in channel i
Rs is the resulting correlation coefficient.
As to the computation expenses, for 3-channel ECG with sampling frequency 400 Hz in real-time processing, they were 0.17% of processor load (AMD Turion II P520 (2.3 GHz), OS Windows 7, 3 GB RAM, single thread native C++ code).
Obviously, the described algorithm must ensure correct detection of QRS complexes in the cases when this problem cannot be solved by any other methods. Let us try to confirm this statement experimentally. We will use a Holter recording made on an old American device. Sampling frequency 128 Hz, insufficient dynamic range, linear oversampling to frequency 400 Hz, rather large degree of noise, there are motion and electrode artifacts, which imitate QRS complexes quite well.
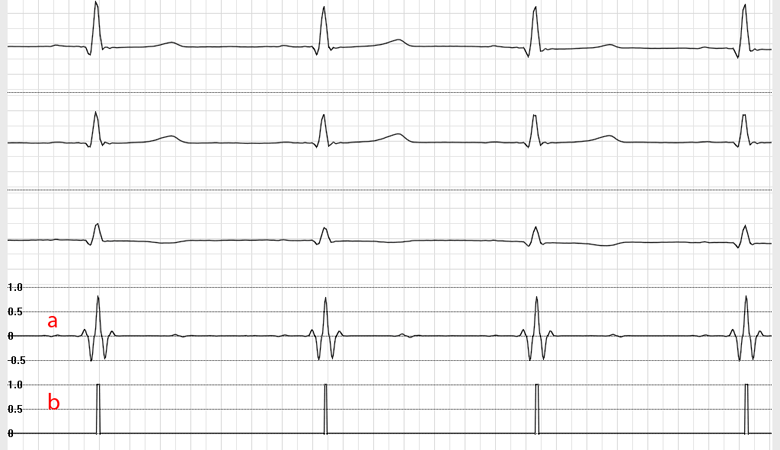
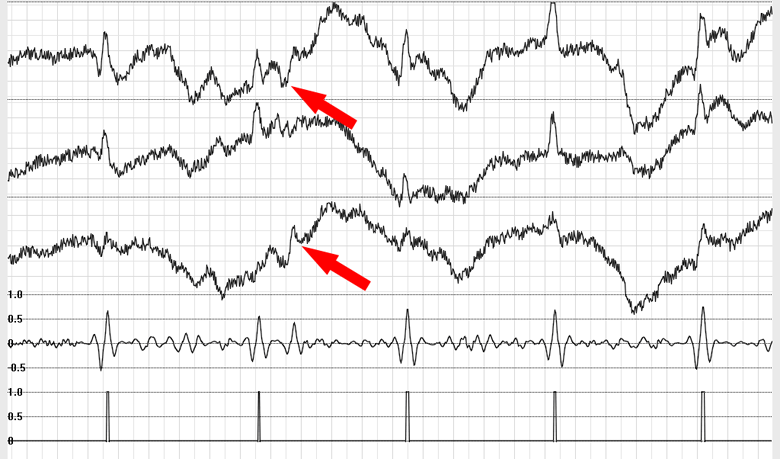
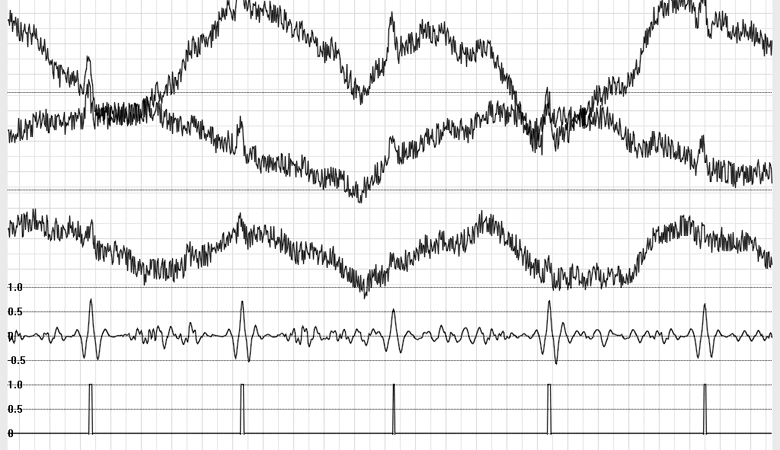
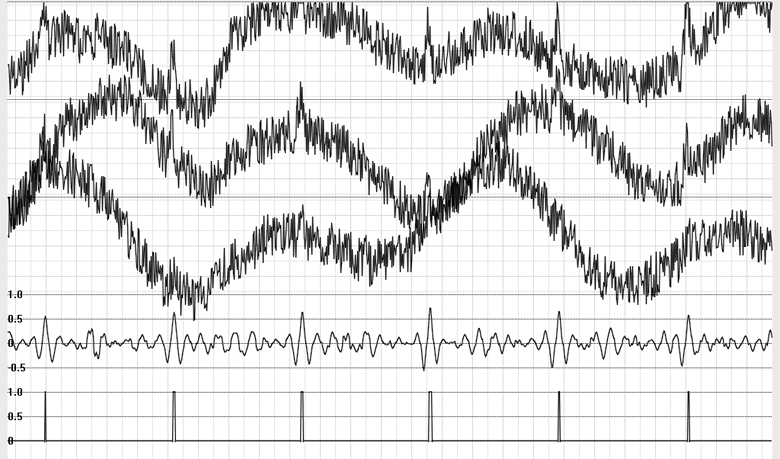
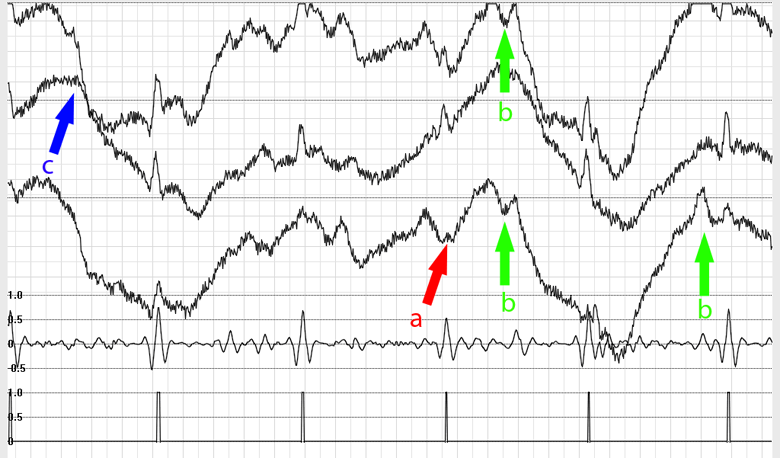

Fig. 8. Fragment of artifact-free Holter recording. Curve 'a' is the output Pearson's correlation coefficient, curve 'b' is the result of decision making, i.e. detection of QRS complex.

Fig. 9. Fragment of recording with pronounced trends, noise and motion artifacts. Imitation interference of natural origin (marked with arrows). The QRS complex detector works correctly.

Fig. 10. Additionally added additive noise of uniform distribution. The detector works correctly.

Fig. 11. Further increase of noise level; additionally added is the low-frequency signal providing trends going outside the equipment dynamic range. The detector still works correctly.

Fig. 12. Recording fragment the most difficult for analysis. Arrow (а) marks the place of completely total disappearance of QRS. Visual detection is hampered. Nevertheless, the used algorithm ensures error-free detection of required signal both on the background of naturally appeared imitation interference (b) and high-amplitude low-frequency artifacts (с).
Conclusions: according to our opinion, the proposed convolution-correlation algorithm ensures close to energy optimum detection of QRS complexes, which cannot be achieved by other ways even theoretically Using Pearson's correlator and eliminating the automatic gain control unit, we minimize the risk of errors of the first and second kind. The realization of Kotelnikov's principle makes it possible to proceed to the complex recognition at the very early stage, almost simultaneously with detection. The utilization of the prototype adaptation system enables us to adjust after a short time the reception algorithm for the most efficient signal detection taking into account individual features of the patient's electrocardiogram. The computation complexity and requirements to processor capacity remain thereat within permissible limits for modern hardware.
References
[1] - Correlation reception and adaptive filtering (in Russian)
[2] - Optimum receiver of completely known signals (in Russian)
[3] - Article "Quasi-optimal numeric rejector filtering of mains interference and its harmonics" (in Russian)
[4] - Article "Double correlation reception of a symmetrical pulse under conditions of AWGN"
Category:
- Log in to post comments
PO box 11515, 61001 Kharkov Ukraine,
tel./fax: +38(050)0113940, +38(057)7290409
E-mail: tredex@tredex-company.com
tredex.office@gmail.com