Категории публикаций
Публикации - Инженерные аспекты
Использование геометрических симметрий для эффективного обнаружения малозаметных целей
26.06.2012
А.В. Крамаренко
Фон Нейман подал мне интересную идею: вовсе не обязательно быть ответственным за тот мир, в котором живёшь. В результате совета фон Неймана я развил очень мощное чувство социальной безответственности.
Ричард Фейнман
Впрочем, наше дело маленькое. Наше дело - прокукарекать, а там хоть не рассветай!
Владимир Богомолов
Пусть есть идеализированный радиолокатор, задачей которого является обнаружение цели с ЭПР, стремящейся к очень малым значениям. Шумы приемного блока локатора предполагаем неизменными и ненулевыми, накопление данных при использовании многократной локации не допускается. Будем считать также, что размер блестящей точки цели пренебрежимо мал в сравнении с пятном «карандашного» луча. Метод обнаружения и выбор порога принятия решения предполагаем близкими к теоретическому оптимуму.
Понятно, что в таком случае эффективность обнаружения при неизменных ЭПР цели и излучаемой станцией мощности будет зависеть только от соотношения S/N (отраженный от цели сигнал/шум). Улучшить характеристики обнаружения невозможно никаким способом, т.к. соотношение сигнал/шум в рамках изложенной задачи изменить нельзя.
Предположим, однако, что существует метод, позволяющий повысить эффективность обнаружения цели при указанных условиях. Допустим также, что он не входит в противоречие с базовыми положениями теории, которая, в сущности, предназначена для ограниченной мерности пространства, в котором производится обнаружение сигнала. Для этого рассмотрим процесс обнаружения в виде геометрической модели.
Будем считать, что луч в картинной плоскости имеет гауссово распределение плотности потока мощности. Тогда единичное «пятно» будет выглядеть следующим образом.

Рис.1. Распределение мощности луча в картинной плоскости
Третьим измерением этого пятна будет дальность, и мы вправе полагать, что в трехмерном пространстве распределение плотности потока мощности будет представлять собой размытый конус, эквимощностные линии которого совпадают с основным лепестком диаграммы направленности антенны.

Рис.2. Распределение мощности в луче
Распределение мощности отраженного от цели сигнала во времени (если блестящая точка находится на продольной оси конуса) соответствует сигналу на входе приемника, причем момент отклика от цели соответствует расстоянию от цели до антенны.
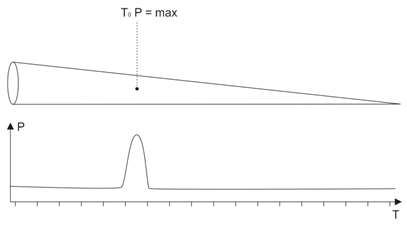
Рис.3. Дальность до цели имеет однозначное соответствие со временем появления отклика от цели
Т.о. мы вправе «заполнить» конус значениями ППМ полученными в результате локации в направлении цели. Т.е., грубо говоря, сигнал на входе приемника может быть преобразован в геометрический объект, где время задержки сигнала перемножается на его скорость распространения в пространстве и становится дальностью, а мгновенная амплитуда сигнала преобразуется в интенсивность заполнения конуса. В результате «яркость» конуса максимальна на дальности, равной дальности до цели, а на остальных дальностях она пропорциональна мгновенной амплитуде шумов на входе приемника.
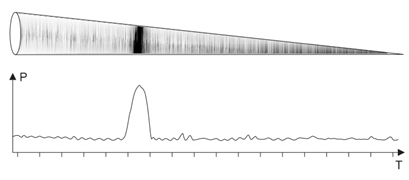
Рис.4. Учитывая однозначное соответствие время/дальность, трансформируем сигнал на входе приемника в заполнение геометрического объекта
В картинной плоскости результат будет представлять собой размытое пятно цели, квантованное лучами, которые и формируют изображение. В данном случае рассматривается уже не один луч, а их совокупность, прошедшая через данную картинную плоскость. То, что они прошли через плоскость разновременно, не представляет для нас интереса – будем считать, что все данные запомнены в некоторой виртуальной памяти (например, в картинной плоскости находится нечто вроде фотоэмульсии, засвечиваемой лучами). При этом отраженный от цели сигнал запоминается тоже.

Рис.5. Распределение эквимощностных линий: цель находится в точке, обозначенной крестом. Полученные сложные фигуры определяются местом нахождения цели относительно решетки лучей. Обратим внимание, что по мере уменьшения мощности отклика от цели, линии стремятся превратиться в окружность.
Для картинных плоскостей, смещенных относительно дальности до цели, распределение принятого сигнала будет стремиться к случайному, обусловленному шумами эфира, шумами приемника и помехами (если они есть).
В итоге, в трехмерном пространстве при апостериорном анализе результатов локации отклик от цели можно рассматривать как эллипсоид вращения.
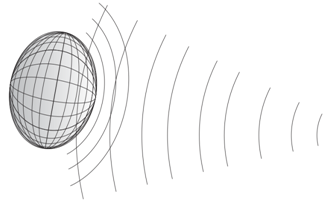
Рис.6. Мы вправе представлять отклик от цели в виде размытого эллипсоида
Если полагать размер блестящей точки пренебрежимо малым, то поперечный размер этого эллипсоида практически полностью определяется шириной главного лепестка ДНА, степень сжатия – отношением ширины лепестка к ширине отклика от цели (во временной области), а яркость – ЭПР блестящей точки.
Понятно, что эллипсоид находится не в пустом сигнальном пространстве, а в пространстве, заполненном действительными сигналами и псевдосигналами, мнимая мощность которых определяется уровнем шумов приемника, а действительная мощность - шумами эфира и помехами. Также очевидно, что и сам эллипсоид имеет аддитивный стохастический компонент, обусловленный теми же шумами.
Но лучи локатора квантуют пространство и при анализе результатов локации некоторого объема пространства мы вправе представить входные запомненные данные в виде трехмерной матрицы, а отраженный от цели сигнал - в величинах яркости вокселов [1], заполняющих весь анализируемый объем. Вводимое понятие воксела (применительно к данной задаче) можно определить как геометрический объект, глубина которого соответствует разрешению локатора по дальности, а размеры в картинной плоскости – разрешению, обусловленному перекрытием лучей. Тогда отклик от блестящей точки можно представить так, как это изображено на рис 7.
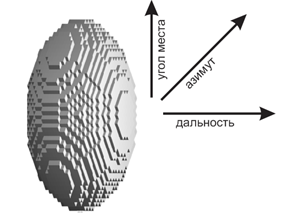
Рис.7. Вследствие импульсного метода работы локатора его лучи квантуют пространство, и эллипсоид мы можем представить только в виде облака вокселов, каждый из которых представляет собой объем пространства, минимальная величина которого обусловлена пределом разрешения системы. Т.е. о распределении мощности внутри воксела мы ничего знать не можем.
Обратим внимание, что заполненная сигналами область пространства вокруг точки, имеющей координаты цели, полностью симметрична относительно этой точки (если эллипсоид вырожден в сферу) и потенциально симметрична для любого эллипсоида при соответствующем пропорциональном сжатии, либо растяжении пространства.
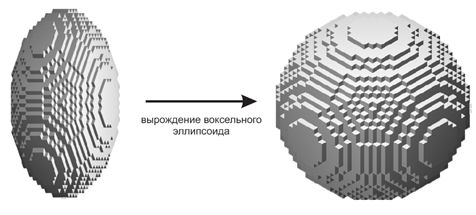
Рис.8. Виртуальное преобразование несимметричного воксела к симметричному (если разрешение по дальности, допустим, лучше разрешения по азимуту/углу места) позволяет упростить расчет яркости слоев эллипсоида
Но для описания симметричного (относительно центра во всех измерениях) объекта достаточно иметь распределение мощности сигнала вдоль эвклидова расстояния (для случая шара - радиуса). В то же время мы имеем избыточное количество информации, полученной в результате локации. И если обеспечить трехмерную свертку полученного сигнала с его трехмерным прототипом, определенным характеристиками априорно известной модели эллипсоида, то отношение S/N (сигнал/некоррелированный с моделью шум) будет обусловлено не только входным S/N отношением, но и корнем квадратным из числа вокселов, из которых состоит модель (в реальных условиях закономерность несколько сложнее). Иными словами: чем уже диаграмма направленности антенны, чем лучше разрешение по дальности и больше объем модели, тем более эффективное когерентное накопление некогерентного шума будет обеспечено. И в сравнении с классическим методом, когда оптимальным обнаружением считается только свертка вдоль одного измерения (дальности), предлагаемый метод обеспечит существенный выигрыш. Понятно также, что если использовать симметрию только в апертуре цели [2], то предельный выигрыш соотношения сигнал/шум ограничен имеющейся мерностью. Если, кроме того, использовать окружающее цель пространство (в предположении, что его ближняя от цели область свободна от других целей), то его три измерения позволяют получить еще более значительный выигрыш.
Однако, многомерная свертка (даже в БПФ варианте) - весьма ресурсозатратное решение. Поэтому выгоднее использовать внутреннюю симметрию принудительно вырожденного эллипсоида и «упаковать» его в одно измерение. Поясним: если разрешение локатора по дальности и азимуту/углу места одинаково, то никаких проблем не возникает. Но обычно разрешение по дальности выше и эллипсоид получается сжатым по соответствующей оси. И самым простым способом использования послойной симметрии будет признание изначально сжатого воксела кубическим т.е. мы будем просто «растягивать» пространство в окрестности цели.
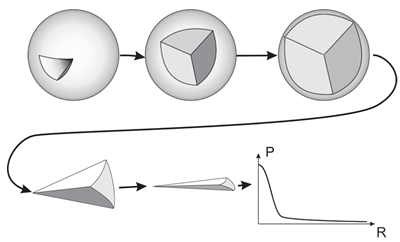
Рис. 9. Суммирование вокселов, относящихся к данному слою, можно представить как разворачивание и сжатие шара.
В вычислительном плане это будет эквивалентно суммированию всех значений мощности для равных значений радиуса. Решение такой задачи табличным способом не будет связано со сколько-нибудь значительными вычислительными затратами.
В итоге получается график, описывающий уровень сигнала в зависимости от удаления воксела от блестящей точки.
Рассмотрим ожидаемый вид этого графика для случая реального использования. Предполагаем, что локатор на каждом следующем такте смещает луч по азимуту и/или углу места на величину половинной мощности ДНА. Тогда величина отклика от блестящей точки на выходе приемника будет иметь амплитуду в 1.414 меньше на следующем такте, в 2 раза на втором и т.д. Т.е. отсчеты по оси ординат будут иметь значения 1.0…0.707…0.5…0.354…0.25 и асимптотически приближаться к нулю.
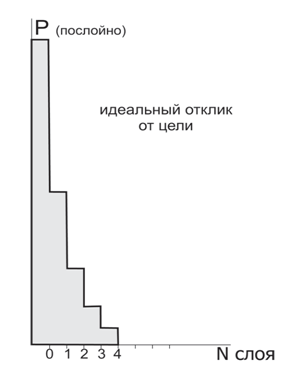
Рис.10. Средняя мощность сигнала в слоях, соотнесенная с максимально возможным откликом от цели (слой №0).
Но т.к. яркость равноотстоящих от центра эллипсоида вокселов эквивалентна (вследствие полной симметрии фигуры), то величину соотношения сигнал/шум в его слоях можно представить следующей таблицей:

Из таблицы следует, что в результате усреднения сигналов во всех вокселах слоя получается снижение уровня шума в корень квадратный из числа суммированных вокселов раз (предполагается, что шум не коррелирован). Вследствие более быстрого падения амплитуды шума относительно падающей амплитуды сигнала во всех слоях, кроме нулевого, обеспечивается более чем трехкратное улучшение соотношения сигнал/шум. В нулевом слое, т.е. центральном вокселе, этого, понятно, не происходит. Если суммировать данные, полученные во всех слоях, то амплитудное соотношение сигнал/шум в данном случае можно повысить еще вдвое. Но это приведет к падению пространственного разрешения всей системы, что неприемлемо (т.е. получится, что мы используем не один луч, а столько, сколько в модели слоев, и разрешение по азимуту/углу места падает пропорционально).
Если же изменить принцип сканирования и/или увеличить перекрытие лучей, то соотношение сигнал/шум дополнительно вырастет без падения разрешения (и это, пожалуй, один из самых полезных «бонусов» предлагаемого метода).
Здесь, впрочем, следует дать некоторые пояснения. Т.к. из таблицы следует парадоксальный (на первый взгляд) вывод о том, что работа по цели более эффективна для случаев, когда антенна «смотрит немного в сторону», то экспериментальное доказательство будет совсем не лишним.
Зададим произвольное (заведомо малое) соотношение сигнал/шум на выходе демодулятора (но до порогового устройства).
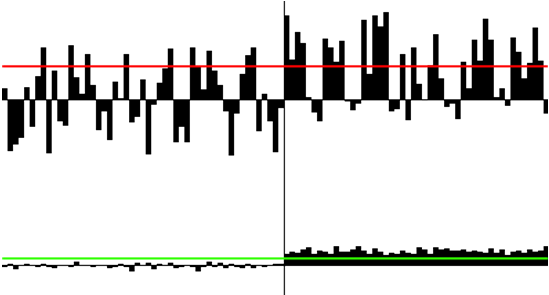
Рис. 11. Верхний график – значения сигнала при измерении в центральном вокселе, нижний – сумма сигналов в вокселах всех слоев, за исключением центрального. По оси абсцисс – время, по оси ординат – квантованные уровни выхода демодулятора. Левая часть графиков соответствует отсутствию полезного сигнала на входе, правая – появился постоянный сигнал во всех вокселах. Его уровень падает по мере удаления от центрального воксела в соответствии с ДНА.
Рис.11. иллюстрирует (для моделирования была использована специально разработанная программа) случай, когда измерения в центральном вокселе (т.е. классический радиолокационный метод) не позволяют выбрать байесов порог, обеспечивающий приемлемую величину ошибок первого/второго рода. Т.е., грубо говоря, сигнал вообще не обнаруживается. В то же время, нижний график демонстрирует своевременное и безошибочное обнаружение сигнала на фоне шумов. Разумеется, при многократной локации и накоплении данных можно обнаружить сигнал и обычным способом, но поставленная задача – не использовать накопления – исключает такой вариант.
Конечно, в данном случае используется простейший набор коэффициентов, который предполагает, что ДНА антенны будет такой:
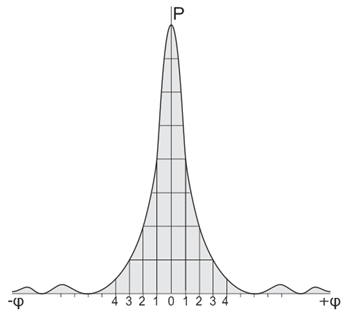
Рис. 12. Диаграмма направленности антенны, которая соответствует коэффициентам, примененным в рассматриваемой модели.
Понятно, что реальная диаграмма направленности будет отличаться, и коэффициенты сигнал/шум в слоях будут иными. При этом следует учесть, что адаптация алгоритма сканирования с учетом особенностей ДНА может дать значительно больший выигрыш в уровне сигнала относительно шумов. Тем более, если метод сканирования будет иметь половинное смещение строки в четных и нечетных столбцах – тогда заполнение станет гексагональным, а воксел - шестиугольной призмой. Впрочем, рассмотрение вопросов оптимизации метода представляется пока преждевременным.
В результате выполнения описанного геометрического преобразования будет получен сигнал, описывающий соответствие принятых данных модели. При этом степень соответствия прототипу эквивалентна вероятности нахождения цели в точке пространства, которая совпадает с центром модели.
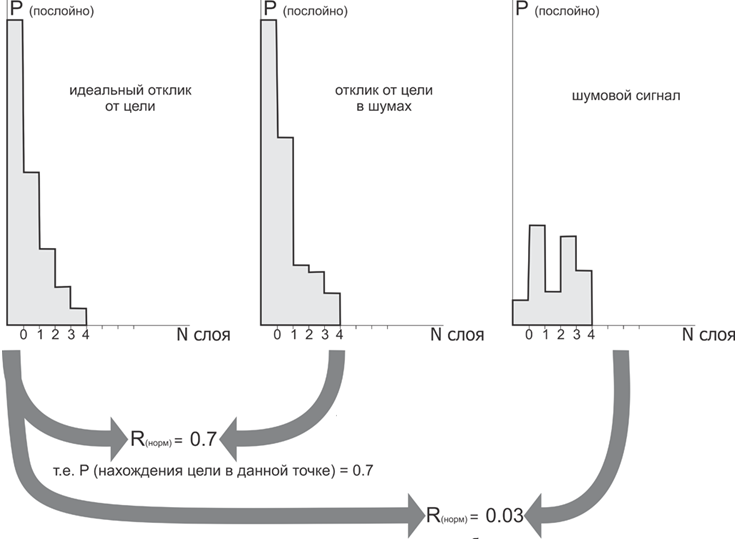
Рис.13. Алгоритм принятия решения при сравнении послойных откликов от цели. Здесь R(норм) – значения пирсоновского корреляционного коэффициента и одновременно вероятность нахождения цели в точке с координатами, совпадающими с координатами центрального воксела. Отклик от цели всегда сравнивается с эталоном, т.е. идеальным откликом.
Вычисление нормированной корреляции полученной последовательности с эталонной (которая соответствует идеальному отклику от цели) трансформирует все данные в одно выходное значение, что эквивалентно усреднению для некоррелированных процессов.
Не забудем, что и сигнал и прототип должны быть перемножены на весовое окно данных, представляющее собой коэффициенты сигнал/шум для соответствующих слоев.
Т.о. можно с хорошим приближением предполагать, что влияние шума будет снижено в корень квадратный из числа анализируемых слоев эллипсоида раз. В нашем случае это будет не менее чем двукратное амплитудное отношение. А итоговый выигрыш может быть оценен как шестикратный амплитудный, т.е. в 36 раз по мощности. Для оптимального алгоритма сканирования и адаптированной к предлагаемому методу ДНА выигрыш будет еще более значительным, но, по мнению автора, такая работа представит собой значительную математическую сложность. Не исключено, тем не менее, что простое и красивое решение существует.
Последовательно смещая модель (отставание от текущей локации составит количество тактов, равное половине потребного числа вокселов), мы получаем обычный результат локации, но со значительно лучшим соотношением сигнал/шум, что обеспечит и повышенную дальность обнаружения целей, и большую стойкость к АБГШ помехам.
Если же вместо пирсоновского коррелятора использовать обычный метод вычисления свертки сигнала с его прототипом, то выходные данные будут получены в более привычном формате, который хотя и требует нормировки по выходным амплитудам, но и дает возможность оценить энергию отклика от цели. В этом случае необходимо оценить ожидаемую величину пространственного разрешения всей системы с учетом введения послойной модели. Учтем, что в классическом методе разрешение по азимуту/углу места определяется шириной главного лепестка ДНА и коэффициентом перекрытия лучей, а в предлагаемом методе – сверткой идеального послойного отклика от цели с самим собой.
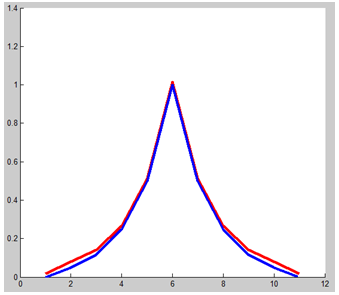
Рис.14. Дискретный отклик от цели, обусловленный ДНА (на Рис. 12). Красная ломаная – обычный метод обработки РЛ данных, синяя – свертка идеального отклика от цели (Рис.10), т.е. предлагаемый метод. Следует ожидать, что отличия в получаемом изображении цели будут невелики, а пространственное разрешение не только не упадет, а даже несколько улучшится.
Необходимо также отметить, что повышение соотношения сигнал/шум обеспечивается в предлагаемом методе исключительно геометрией и легко поддаётся приближенному расчёту, хотя, конечно, правильнее было бы сопоставлять лапласианы различных мерностей.
Попробуем экспериментально подтвердить приведенные цифры. Для этого используем модель с предварительно записанной шумовой последовательностью и будем повышать уровень шума до того момента, когда количество ошибок первого и второго рода будет сохраняться нулевым у предлагаемого метода. Затем, понижая уровень шума, добьемся нулевого количества ошибок и для классического метода.
Здесь следует оговориться, что такой подход к задаче не вполне корректен, более того, подобное фамильярное обращение с шумоподобными сигналами является дурным тоном, но, тем не менее, эксперимент позволит получить грубую приближенную оценку и одновременно избежать многих страниц аналитического доказательства.
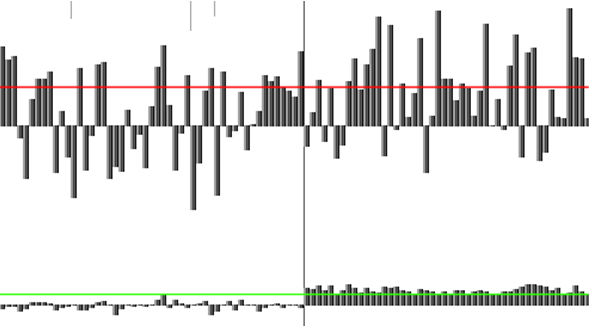
Рис. 15. Уровень шума таков, что только предлагаемый метод (график внизу) обеспечивает нулевое количество ошибок при обнаружении сигнала (для данной шумовой последовательности, разумеется). Необходимо еще раз заметить, что дополнительными методами обработки можно выделить полезный сигнал и из верхнего графика, но это потребует накопления данных, а в нашем случае многократная локация не допускается по определению.
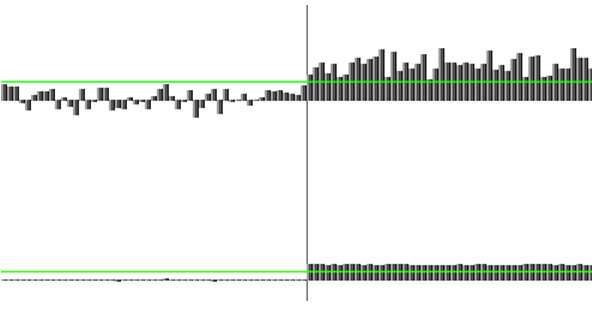
Рис.16. Для того чтобы классический метод «вышел» на нулевое количество ошибок (для той же шумовой последовательности) нам пришлось уменьшить амплитуду шума в пять раз. Уровень сигнала, понятное дело, не изменялся.
Полученный коэффициент неплохо согласуется с предыдущей оценкой – дело в том, что здесь мы раздельно используем данные от центрального воксела и суммированные послойные данные. При использовании данных всех слоев, включая нулевой, мы можем надеяться именно на шестикратный выигрыш в амплитудном соотношении сигнал/шум.
Попробуем с помощью программной модели проиллюстрировать полученный результат применительно к треку цели. Пусть ЭПР цели увеличивается от нуля до некоторого произвольного значения (так, что амплитуда сигнала линейно растет на входе), при котором трек становится непрерывным для обоих методов обработки РЛ сигнала (Рис.17).
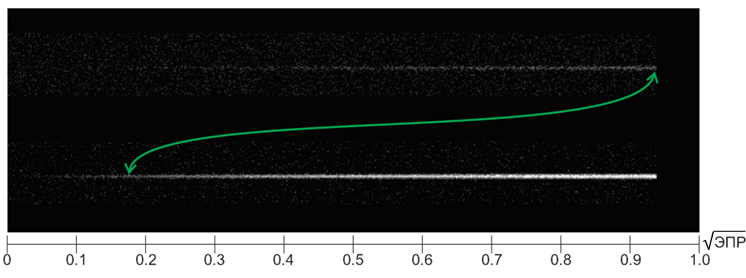
Рис.17. Треки целей с линейно увеличивающейся ЭПР на фоне шумов. Сверху – обычный способ обнаружения, внизу – предлагаемый. Сигнал до порогового устройства. Уровень шумов нормирован, т.е. изображения можно сравнивать.
Очевидно, что предлагаемый метод позволяет получить без когерентного накопления сигнала не менее чем двадцатипятикратный выигрыш в величинах ЭПР и, соответственно, увеличение дальности обнаружения цели в 2,2 раза при неизменной мощности передатчика и чувствительности приемника. Что, несомненно, оправдает попытки его применения в реальной практике. Хотя, эта самая реальная практика, будучи задействованной, любит преподносить проблемы. Например, для высокоскоростной цели и/или очень большой дальности до цели возникнет проблема деформации эллипсоида в связи с тем, что за время потребных тактов локации цель успеет сместиться. Адаптация ДНА к предлагаемому методу и оптимизация коэффициентов, а также выбор наилучшего способа сканирования тоже будет тем еще подарком. Хотя и перспективным…
Итак, алгоритм работы устройства (программного, аппаратная часть не изменяется) будет выглядеть примерно следующим образом:
С выхода демодулятора приёмника (но до порогового обнаружителя) сигнал подаётся на ЗУ, которое в соответствии с методом сканирования заполняет ячейки памяти принятыми значениями. В нашем случае требуется 9х9х9 элементов. По заполнении всех ячеек производится взвешенное суммирование сигналов в вокселах, относящихся к слоям соответствующих номеров и на выходе получается таблица яркости слоёв. Эти значения подаются на пирсоновский коррелятор, прототипом для которого является таблица яркости слоёв, экспериментально полученная данным локатором для единичной малоразмерной цели в условиях отсутствия помех. Выходное значение нормированной корреляции представляет собой вероятность обнаружения цели в точке, соответствующей центру эллипсоида. Цикл повторяется по мере накопления данных и смещения анализируемой точки.
Т.о. вероятность нахождения цели в точке с координатами x, y, z будет определена указанным ниже способом.

В случае если необходимо получить значение яркости блестящей точки может быть использована обычная свертка послойного отклика от цели с эталоном, и результат подан на нелинейное устройство, формирующее байесов порог.
В качестве заключения можно привести следующее:
Предлагаемый метод не является вариантом улучшения сигнал/шум, связанным с управлением лучом. Т.е. существующие методы прицельного анализа угрожаемых секторов, многократной локации выбранного сектора, «прожигание помехи» и т.д. и т.п., в сущности, всегда предусматривают адаптивное управление методом сканирования. Метод использования геометрических симметрий не требует изменения алгоритма сканирования во время работы, и поэтому дополняет указанные классические методы и может использоваться одновременно с ними. Улучшение соотношения сигнал/шум в этом случае будет перемножаться (пожалуйста, NB!).
Ожидаемый выигрыш по соотношению сигнал/шум приведет к многократному эквивалентному повышению ЭПР цели, что, скорее всего, во многом обессмыслит «Stealth» технологию, т.к. достижение сверхмалых ЭПР и так уже достигло почти теоретического предела. А необходимость понизить ЭПР еще в несколько раз, кроме физических ограничений, имеет еще и экономические. Впрочем «ужастики» о лобовой атаке подготовленной современной ПВО только малозаметными ЛА «в чистом небе», т.е. без прикрытия активными помехами и так относятся к области компетенции желтой прессы.
Как представляется автору, метод может оказаться полезным при встречном дальнем обнаружении ЛА друг друга. Эквивалентный выигрыш в десятки раз по мощности и в два раза по дальности при одинаковых ЭПР ЛА однозначно позволит получить тому из них, который использует предлагаемый метод, решающее преимущество в выборе момента и метода атаки. Но вопросы тактического применения не относятся к компетенции обработчика сигнала.
Самым существенным и принципиально важным, на мой взгляд, преимуществом будет возможность получения (с помощью нормированной корреляции) РЛ изображения в виде плотностей вероятности нахождения цели. Тогда, обработав в качестве гипотезы все физически непротиворечивые треки целей (о вычислительных затратах умолчим) и взяв интеграл по треку, мы сможем дополнительно многократно понизить порог обнаружения на фоне шумов.
Категории:
- Войдите, чтобы оставлять комментарии
Адрес: Украина, 61057, Харьков, а/я 39,
тел./факс.: +38(050)0113940, +38(057)7290409.
E-mail: tredex@tredex-company.com
tredex.office@gmail.com
Комментарии
Александр
12.02.2013 - 18:45
Постоянная ссылка (Permalink)
Вынужден принести извинения. В одном месте был пропущен знак квадратного корня, в другом был неправильный коэффициент. Исправлено.
К счастью, этого никто, похоже, не заметил.
nikolay
13.05.2015 - 08:28
Постоянная ссылка (Permalink)
Добрый день! Уважаемый Александр!
Пусть у меня есть выборка амплитудных значений по дальности, соответствующая определенному азимутальному положению антенны. Пусть в j-ом элементе массива присутствует сигнал цели. Не могли бы Вы пояснить как вычисляется корреляционный порог обнаружения для этого случая?
С уважением, Николай.
Александр
16.05.2015 - 19:48
Постоянная ссылка (Permalink)
" Пусть в j-ом элементе массива присутствует сигнал цели. "
Разумеется, если сигнал присутствует только в j-м элементе и полностью отсутствует в соседних, то вычисление корреляции теряет смысл. Но это может быть только тогда, когда полоса пропускания усилителя бесконечна или частота дискретизации мала.
В реальности, при выполнении условия Котельникова сигнал будет присутствовать и в j-1 элементе, и в j -2м, и в j +1м и т.д. Тогда отсчеты в окрестностях центрального j-го элемента будут соответствовать точкам на кривой, описывающий отклик системы на цель в размерности "дальность". И эту кривую, понятное дело, можно сравнить с эталонной или эталонными кривыми. Лучше всего для этого подходит (на мой взгляд) пирсоновский коррелятор, т.к. он дает нормированные результаты (АРУ не нужна). Более подробно я описал этот принцип здесь: http://www.tredex-company.com/ru/dvojnoj-korrelyatsionnyj-priem-simmetri...
Практическое применение (правда для совсем другого сигнала) здесь:http://www.tredex-company.com/ru/svertochno-korrelyatsionnyj-algoritm-vy...
Но пожалуйста, имейте в виду, что все это пока не шибко признано специалистами: некоторые одобрямс, некоторые утверждают, что автор ошибается (суть ошибки не указывают). Так что выбор за Вами.