Publication categories
Spectral analysis with variable data window
04/27/2007
Kramarenko A.V.
The classical spectral evaluation is perceived as such well worked out and finished in its development method, that when it is inefficient in solving a specified problem, no other propositions are put forward, but to increase the realization or apply the methods of non-classical spectral analysis.
However, we must not forget that the development of digital methods of calculation of power spectrum took place at the times, when the computational power of processors was extremely small compared with the contemporary one. And the optimization of the method was carried out mainly in the field of speeding up computations and reducing the necessary number of mathematical operations. As to the efficiency of the method itself, its possibilities are virtually completely exhausted by the characteristics of the used data window.
It is quite possible that just because this the author of one of the most required monographs [1] allowed himself a paradoxical (at first sight) statement: "... the practice of implementation of the methods of spectral evaluation using the finite data sets is not a precise science: it is to a great extent based on experimental results and usually requires one or other particular compromises"».
Taking into account this particular opinion, we take the liberty to carry out an experimental verification of the methods of classical spectral evaluation (the author is mentally sound and does not suffer from megalomania, remembers Descartes and just only tries to call in question what came to hand).
Let us specify the following model for 512-dot realization in the floating point format:
frequency_discret=200.0; frequency=9.5; phase=0;
for(i=0;i<512;i++){ data=0.0001*amplitude*sin((2.0*pi/frequency_discret)*(double)i*(frequency*1.4)+phase)+
0.01*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency*2)+phase)+
0.000001*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency*2.5)+phase)+
0.01*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency*0.24)+phase)+
0.1*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency+1)+phase)+
amplitude*sin((2.0*pi/ frequency_discret)*(double)i*frequency+phase);
}
The synthesized signal in time domain will look as shown in Fig.1.
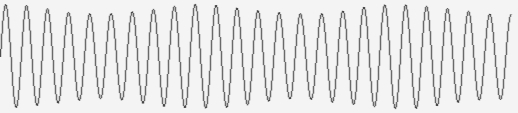
Fig. 1. Additive mixture of monochromatic signals specified by the model at 512-dot realization.
It is also evident that in frequency domain such set of frequency components follows from the conditions of the task (Fig. 2).
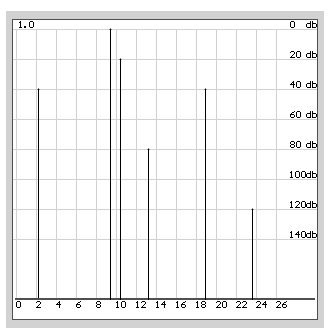
Fig 2. Set of frequency components used for the signal synthesis.
Now let us apply to the synthesized signal the usual method of power spectrum calculation without utilizing the data window (that is it is rectangular). Let us specify a redundant resolution in frequency, so that the width of the main and side lobes is clearly manifested. The results are shown in Fig 3.
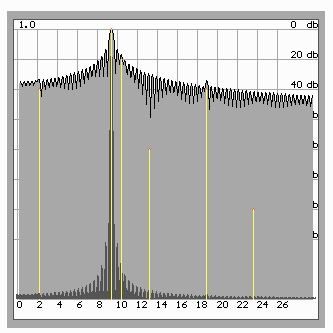
Fig 3. Result of spectral evaluation of the signal in linear (dark color) and logarithmic (gray color) scales. The spectrum is superimposed on the image of the frequency components, which have formed this signal (yellow lines).
It follows from the analysis of the results that the frequency of the main harmonic is determined exactly, while the frequency components with the level below -40 dB are virtually unobservable. Automatic recognition of the closely located component - 20 dB is also impossible. The reason is evident - high level of the side lobes from the main harmonic impedes the detection of frequency components with lower power.
The solution of the problem used in the standard approach supposes the application of the weigh data window, which lowers the level of the side lobes. In this case the frequency resolution of the method becomes lower and the main lobes become wider, which often leads to the refusal to use any data windows at all (Fig 4).
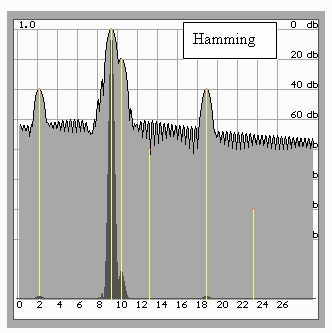
Fig 4. The data window used has made it possible to detect signals -20 and -40 dB with widened main lobes and lowered frequency resolution of the method
Nevertheless, when using the Hamming window it is impossible to detect components below -60 dB. To solve such problems, the Nattoll window is often used (Fig. 5), which makes it possible to detect components down to -100 dB with correspondingly lowered frequency resolution and widened main lobes (effect, inevitable in the classical spectral evaluation).
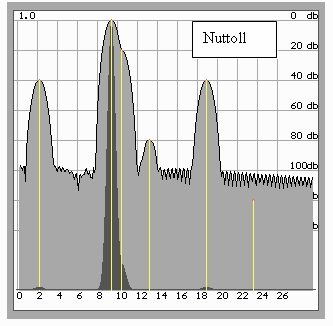
Fig.5. Nattoll window makes it possible to detect a -80 dB signal with even more widened main lobes. Moreover, the detection of the closely located component -20 dB is difficult or impossible due the lowered frequency resolution of the method. Signal -
And just these demonstrated effects contain the main problem connected with the application of data windows in spectral analysis. In a "generally accepted" version, envisaging one-time estimation of available realization, the problem is not solved at all - either the analysis will yield a high resolution and narrow lobes, but a high level of the side lobes, or vice versa. Compromise variants also have the right on life with obligatory a priori knowledge of the characteristics of the signal being investigated, that is, such method of spectral analysis stops to be universal to a smallest extent.
At the same time, the operator, who evaluates obtained results, can compare the data, obtained with the help of various windows. That is, to determine the frequency of the main component from the data, obtained with the help of a rectangular window, low-level components - with the help of Nattoll window, the component located close to the main one - by means of Hamming window and so on. It is also evident that for each spectral component the operation will choose the minimum value from those obtained in various experiments. Such decision is not only intuitively understandable, but also follows from the basic principles of signal conversion from time domain into frequency one.
No need to prove that any leakage of power when computing the spectrum will only lead to the increase of the spectral component, into which the interference "hits". As energy cannot be negative, as the result of any incorrectness of the method the spectral component can only increase in respect to the true value, but in no way lower. That is, at multiple spectral evaluation of one and the same realization the closest to the truth will be the minimum value of any spectral component. Of course, this statement is true only for spectral data normalized in respect to the main component.
Let us try to analyze in automatic mode the available results of spectral evaluation of a test signal, i.e. to compare the normalized spectra and select the minimum values (Fig.6).
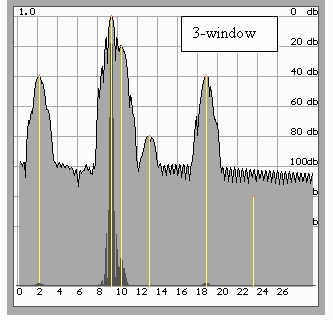
Sequential application of three windows with the selection of the minimum value makes it possible to detect signals -80 dB with widening of the main lobes not exceeding the best values for any of the used windows. Nevertheless, signal -120 dB cannot be
Surely, such decision can be only a palliative, because only three data windows have been used, and their specific features have been totally ignored when obtaining the final results. We must suppose that a more general and universal solution of the problem exists.
If we suppose that in the process of multiple computations of the spectrum of a given realization we can change the data window, then, when choosing the minimum value for each spectral component, namely the window transformation will determine both the maximum level of the side lobes, and the frequency resolution of the method.
It is also obvious, that it is desirable to "start up" with a data window that ensures the minimum level of the side lobes.
It is not difficult to synthesize such window, possessing modern computational powers (Fig.7).
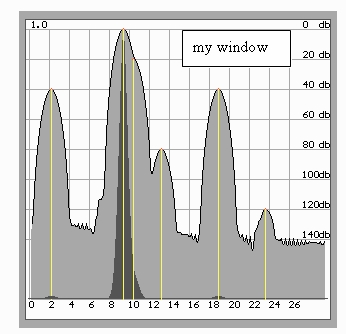
Fig.7. Specially designed window makes it possible to reliably detect signal -120 dB with the main lobes widened even more than with Nattoll window. However, signal -20 dB located close to the main harmonic is not detected due to lowered frequency resol
If we apply this window several times "elongating" it successively, with a section of unit weigh coefficients being added to it, and the edges being proportionally scaled along the X axis (Fig. 8), we can obtain the results, shown in Fig 9.
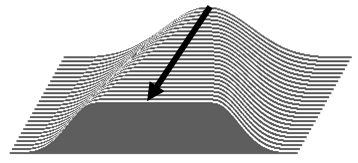
Fig. 8. Transformation of the data window for each successive iteration.
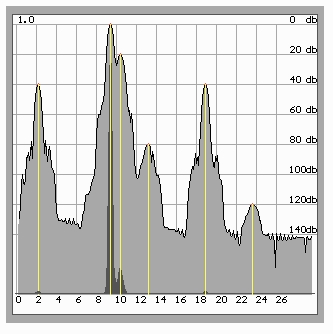
Fig.9. Reliably detected are both signal -120 dB, and signal -20 dB, located close to the main harmonic. The width of the main lobes is smaller than in all windows used in the traditional approach, except the rectangular one.
It is obvious, that even after just 16 iterations the obtained spectrum is much closer to the specified model, than any one, calculated with the help of the traditional windows (surely, within the scope of the classical methods of spectral evaluation).
We obtain even more convincing results, if we continue to widen the window. Increasing the number of iterations up to 32 enables us to obtain not only narrow main lobes, but also to reach an excellent (down to -60 dB!) separation of two closely located signals, which is absolutely impossible with any of the known spectral windows.
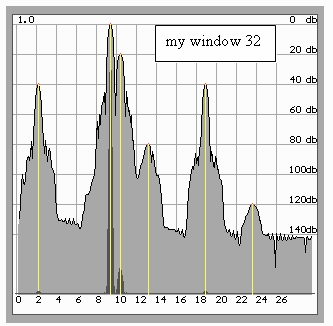
Fig 10. Reliable (down to - 60 dB) separation of signals 0 dB and -20 dB. The width of the main lobes even smaller than at 16 iterations.
Further increase of the number of iterations and, as a consequence, even greater widening of the window lead to even greater narrowing of the main lobes, this effect thereat reaching paradoxic (at first glance) values. You can easily see in Fig.11 that the main lobe with the suggested method of spectral evaluation is narrower than when the rectangular data window is applied. Perhaps, this effect will open additional possibilities in the application of the classical methods of spectral evaluation.
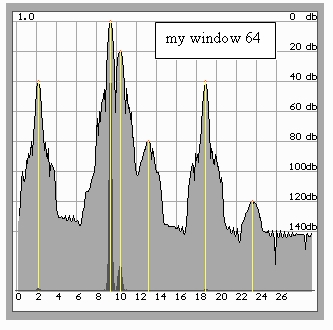
Fig 11. The width of the main lobes is smaller than when the rectangular window is used. You can see that the upper part of the lobe narrows till it coincides with the line (marked yellow) to the frequency of spectral components of the specified model,
As the result of application of the method of utilization of a variable data window, the task of separation of all spectral components is completely solved. It is absolutely impossible when using the classical approach with one-time analysis of the realization and when selecting any of the existing at present data windows.
It is not excluded that this problem can be solved also by using non-classical methods of evaluation (autoregressive, etc.) However, please do not forget that autoregressive methods investigate, in fact, not the realization itself, but the model created on its basis, that is they do not provide the complete substitution of the methods of classical spectral analysis.
Thus, we can suppose that the method proposed by the author substantially widens the possibilities of the classical methods of spectral analysis, without going beyond the base theory. The inevitable increase of the number of mathematical operations necessary for the spectrum calculation (from several to dozens of times) does not constitute a substantial drawback of the method. The computational power of modern computers of any level makes it possible to solve even more labor-consuming problems in real time. Besides, it follows from the method itself, that the process can be easily parallelized and in this case the expenses on providing a spectral analysis will be transformed into an insignificant increase of the cost of hardware. Let us also note that no contradiction with the basic principle uncertainty arises when the proposed method is used. The frequency resolution only approaches its theoretical limit, but not surpasses it.
However, optimism is inherent most often to incompetent and pathologically energetic “inventors”. Therefore, forestalling possible criticism and suspicion in incompetence or clinical dilettantism, we must say that the spectrum, when it is calculated with a varying window, really looks somewhat odd. The lobes of relatively high energy have the shape resembling church bell towers – narrow at the top and stepwise widening at the bottom. At the same time the low-energy components do not have this form, but are widened in respect to more powerful components. The cause of these effects is the used method of window transformation, that is, the widening of the window when a rectangular section is inserted (as if a terrier dog is stretched to a basset) is knowingly not the optimal method of transformation. Scholars do not succeed to solve this problem yet due to its considerable mathematical complexity. Although, of course, the method of optimal transformation of the window exists, and when it is used, all lobes will take an inviting to eye appearance.
From my point of view, the practical application of the proposed method can be very wide: from spectral analysis in radiolocation to investigation of electroencephalogram. Let us try to apply it to a standard EEG of a healthy person.
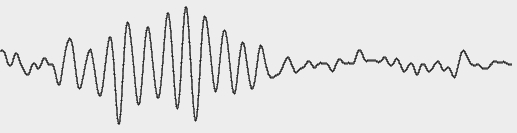
Fig. 12. EEG with pronounced well-modulated alpha rhythm with frequency about 10 Hertz. 16-digit quantization, sampling frequency 200 Hertz.
Let us perform a spectral analysis of this realization by the standard method using Hamming window. The left-hand picture presents the spectrum (Fig. 13). Domination of alpha rhythm is vividly manifested, another rhythmical activity is also presented in full correspondence with EEG characteristics of a healthy person. On the spectrum obtained using the proposed method the picture is substantially different. While the main spectral components coincide with the previous data both as to frequencies and level, the minimums of spectral densities differ rather significantly. It is amazing, but the minimums virtually exactly fall in the areas of rhythm separation described by classical electrophysiology. So, clear separation of delta activity (0.5 – 3 Hz) and theta activity (4 – 8 Hz) is observed. Alpha rhythm is also separated from beta activity, which, in its turn, is well separated into classical beta1 and beta2. The only unexpected is the separation of beta1 activity into two sub-bands.
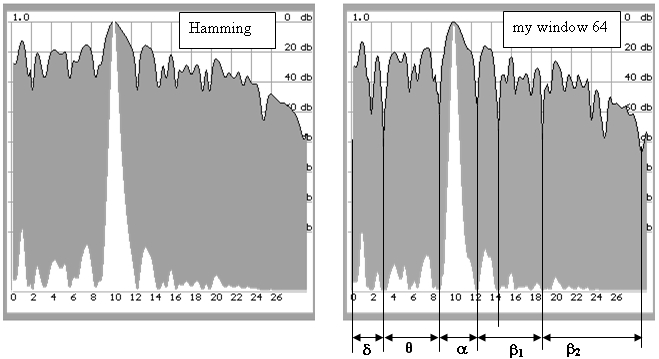
Fig.13. Spectra of shown EGG. Left – Hamming window, right – proposed method.
We must also take into account that the registered minimums (down to -80 dB) at 16-digit quantization and non-zero self-noise of the amplifier unambiguously indicate the complete absence of the brain electric activity at these frequencies (because the amplifier noise and sampling noise give approximately -80 dB, so nothing is left for the true EEG signal). Such fact can be of significant interest to physiologists – the brain does not generate electric signals at very finely tuned frequencies. That is, either EEG is a sum of a large number of rather stable as to frequency generators, or these are Fraunhofer lines caused by antiphase generation. It is very interesting, how these minimums of spectral density behave in time, at functional loads and various diseases. Anyway, with the proposed method we obtain a new quality of electroencephalogram analysis.
So, with some impudence we can suppose that it is permissible to consider the proposed method of spectrum evaluation with varying data window as a development of the classical spectral analysis.
Category:
- Log in to post comments
PO box 11515, 61001 Kharkov Ukraine,
tel./fax: +38(050)0113940, +38(057)7290409
E-mail: tredex@tredex-company.com
tredex.office@gmail.com