Спектральный анализ с изменяющимся окном данных

Классическое спектральное оценивание воспринимается настолько хорошо проработанным и законченным в своем развитии методом, что при неэффективности его применения для решения поставленной задачи не возникает других предложений, кроме увеличения реализации или применения методов неклассического спектрального анализа.

 

Однако не следует забывать, что разработка цифровых методов вычисления энергетического спектра велась во времена, когда вычислительная мощность процессоров была несопоставимо малой в сравнении с современными. А оптимизация метода была проведена преимущественно в области ускорения вычислений и уменьшения необходимого числа математических операций. Что касается эффективности самого метода, то его возможности практически полностью исчерпываются характеристиками примененного окна данных.

 

Вполне вероятно, что именно поэтому автор одной из самых востребованных монографий [1] позволил себе парадоксальное (на первый взгляд) утверждение: «... практика применения методов спектрального оценивания с использованием конечных наборов данных не составляет собой некую точную науку: она в значительной мере основывается на результатах экспериментов и обычно требует тех или иных конкретных компромиссов».

 

Учитывая именно это мнение, позволим себе провести экспериментальную проверку методов классического спектрального оценивания (автор психически здоров и манией величия не страдает, Декарта помнит, и всего лишь пытается подвергнуть сомнению то, что под руку подвернулось).

 

Зададим следующую модель для 512-точечной реализации в формате с плавающей точкой:

 

frequency_discret=200.0; frequency=9.5; phase=0;

for(i=0;i<512;i++){ data[i]=0.0001*amplitude*sin((2.0*pi/frequency_discret)*(double)i*(frequency*1.4)+phase)+

0.01*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency*2)+phase)+

 0.000001*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency*2.5)+phase)+

 0.01*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency*0.24)+phase)+

 0.1*amplitude*sin((2.0*pi/ frequency_discret)*(double)i*(frequency+1)+phase)+

 amplitude*sin((2.0*pi/ frequency_discret)*(double)i*frequency+phase);

 }

 

Синтезированный сигнал во временной области будет иметь вид, представленный на рис. 1.

 

 

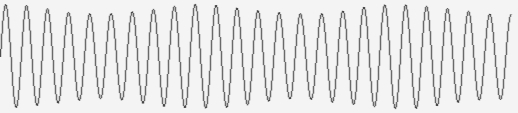
Рис. 1. Аддитивная смесь заданных моделью монохроматических сигналов
при реализации 512 точек.

 

Очевидно также, что в частотной области из условий задания следует такой набор частотных компонентов (рис.2).

 

 

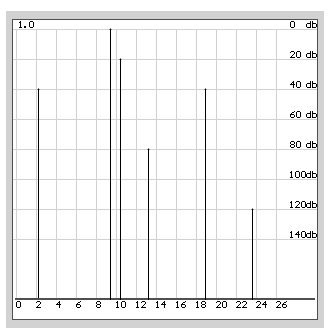
Рис.2 Набор частотных компонентов, использованных для синтеза сигнала.

 

Применим теперь к синтезированному сигналу обычный метод вычисления энергетического спектра без использования окна данных (т.е. оно – прямоугольное). Зададим избыточное разрешение по частоте, чтобы ширина основных и боковых лепестков проявлялась наглядно. Результаты представлены на рис.3.

 

 

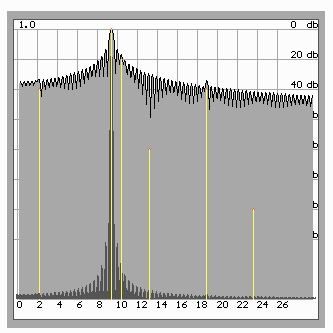
Рис. 3. Результат спектрального оценивания сигнала в линейном (темный цвет) и логарифмическом (серый цвет) масштабах.

Спектр наложен на изображение частотных компонентов, которые образовали данный сигнал (желтые линии).

 

Из результатов анализа следует, что частота основной гармоники определена точно, в то же время частотные компоненты, имеющие уровень ниже –40 дБ практически не обнаруживаются. Автоматическое распознавание близко расположенной компоненты –20 дБ также не может быть проведено. Причина очевидна – высокий уровень боковых лепестков от основной гармоники мешает обнаружить частотные компоненты, которые имеют меньшую мощность.

 

Используемое в стандартном подходе решение проблемы предполагает применение весового окна данных, снижающего уровень боковых лепестков. В этом случае уменьшается частотное разрешение метода и расширяются основные лепестки, что нередко вызывает отказ от использования каких-либо окон данных вообще (рис.4).

 

 

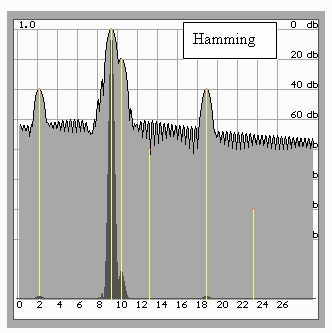
Рис.4. Примененное окно данных позволило обнаружить сигналы –20 и –40 дБ при расширении основных лепестков

и падении частотного разрешения метода

 

Тем не менее, при использовании окна Хэмминга не удается обнаружить компоненты ниже –60 дБ. Для решения подобных задач часто используется окно Наттолла (рис.5), позволяющее обнаруживать компоненты до –100дБ при соответствующем падении частотного разрешения и расширении основных лепестков (неизбежный в классическом спектральном оценивании эффект).

 

  

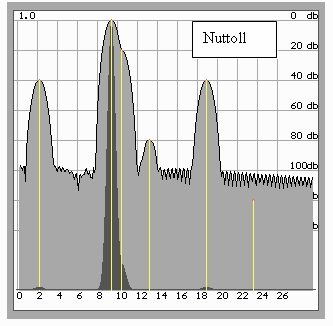
Рис.5. Окно Наттолла позволяет обнаружить сигнал –80 дБ при еще большем расширении основных лепестков.

Вместе с тем, обнаружение близко расположенной компоненты –20 дБ затруднено

или невозможно вследствие падения частотного разрешения метода.

Сигнал –120 дБ гарантированно не обнаруживается.

 

В показанных эффектах и заключается основная проблема, связанная с применением окон данных в спектральном анализе. В «общепринятом» варианте, предусматривающем однократную оценку имеющейся реализации, проблема не решается вообще – либо в результате анализа будет получено высокое разрешение и узкие лепестки, но высокий уровень боковых лепестков, либо наоборот. Компромиссные варианты тоже имеют право на жизнь при обязательном априорном знании характеристик анализируемого сигнала, т.е. такой метод спектрального анализа перестает быть сколько-нибудь универсальным.

 

Вместе с тем, оператор, оценивающий полученные результаты, может воспользоваться сопоставлением данных, полученных с помощью различных окон. Т.е. частоту основной компоненты определить по данным, полученным с помощью прямоугольного окна, низкоуровневые компоненты – с помощью окна Наттолла, близкорасположенную к основной компоненту - с помощью окна Хэмминга и т.п. Очевидно также, что для каждой спектральной компоненты оператор будет выбирать минимальное значение из всех, полученных в разных экспериментах. Такое решение не только интуитивно понятно, но и следует из основных принципов преобразования сигнала из временной области в частотную.

 

Не требует доказательств, что любое просачивание энергии при вычислении спектра будет приводить только к повышению уровня спектральной компоненты, в которую «попадает» помеха. Так как энергия отрицательной быть не может, спектральная компонента в результате любой некорректности метода может только возрастать относительно истинного значения, но ни в каком случае не снижаться. Т.е. при многократном спектральном оценивании одной и той же реализации с разными окнами данных, наиболее близким к истине будет минимальное значение любой спектральной компоненты. Это утверждение справедливо, разумеется, только для нормированных относительно основной компоненты спектральных данных.

 

Попробуем в автоматическом режиме проанализировать имеющиеся результаты спектрального оценивания тестового сигнала, т.е. сопоставить нормированные спектры и выбрать минимальные значения (рис.6).

 

 

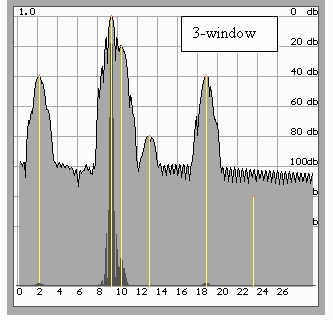
Рис.6. Применение трех окон последовательно с выбором минимального значения позволяет обнаружить сигналы –80 дБ

при расширении основных лепестков, не превышающих лучшие значения для любого из использованных окон.

Тем не менее, сигнал  –120 дБ гарантированно не обнаруживается.

 

Разумеется, такое решение может быть только паллиативом, т.к. использовано всего лишь три окна данных, причем их особенности никак не учтены при получении окончательных результатов. Следует предположить, что существует более общее и универсальное решение задачи.

 

Если допустить, что в процессе многократных вычислений спектра данной реализации можно изменять окно данных, то при выборе минимального значения для каждой спектральной компоненты, именно трансформация окна будет определять как максимальный уровень боковых лепестков, так и частотное разрешение метода.

 

Очевидно также, что «стартовать» желательно с окном данных, обеспечивающим минимальный уровень боковых лепестков.

 

Синтез такого окна при современных вычислительных мощностях не представляет большой трудности (рис.7).

 

 

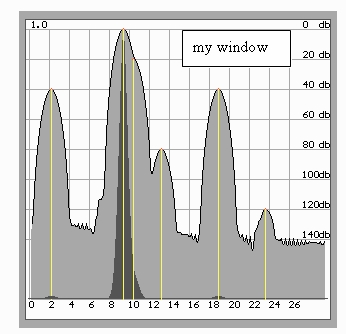
Рис.7. Специально спроектированное окно позволяет уверенно обнаружить сигнал
–120 дБ при еще большем, чем у Наттолла расширении основных лепестков.

Однако, расположенный близко к основной гармонике сигнал –20дБ не обнаруживается вследствие падения частотного разрешения

(все в полном соответствии с теорией).

 

Если применить данное окно многократно при его последовательном «удлинении», когда в него добавляется участок единичных взвешивающих коэффициентов, а края пропорционально масштабируются по оси Х (рис.8), можно получить результаты, показанные на рис.9.

 

 

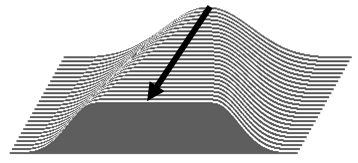
Рис.8. Трансформация окна данных для каждой последующей итерации.

 

 

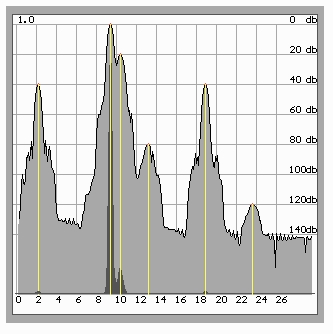
Рис.9. Уверенно обнаруживается как сигнал –120 дБ, так и расположенный близко к основной гармонике сигнал –20 дБ.

Ширина основных лепестков меньше, чем при всех применяемых в традиционном подходе окнах, за исключением прямоугольного.

 

Очевидно, что даже после всего лишь 16 итераций, полученный спектр много ближе к заданной модели, чем любой, вычисленный с помощью традиционных окон (в рамках классических методов спектрального оценивания, разумеется).

 

Еще более убедительные результаты получаются в случае продолжения расширения окна. Увеличение количества итераций до 32 дает возможность получить не только узкие основные лепестки, но и достигнуть отличного (до -60 дБ!) разделения двух близко расположенных сигналов, что абсолютно невозможно ни при одном из известных спектральных окон.

 

 

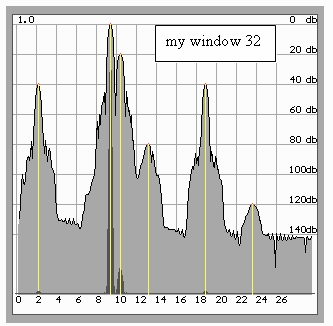
Рис.10. Уверенное (до -60дБ) разделение сигналов 0 дБ и –20дБ. Ширина основных лепестков еще меньше, чем при 16 итерациях.

 

Дальнейшее увеличение количества итераций и, как следствие, все большее расширение окна ведут к еще большему сужению основных лепестков, причем этот эффект достигает парадоксальных (на первый взгляд) величин. На рис.11. легко видеть, что основной лепесток при предлагаемом методе спектрального оценивания имеет меньшую ширину, чем в случае применения прямоугольного окна данных. Этот эффект откроет, вероятно, дополнительные возможности в применении классических методов спектрального оценивания.

 

 

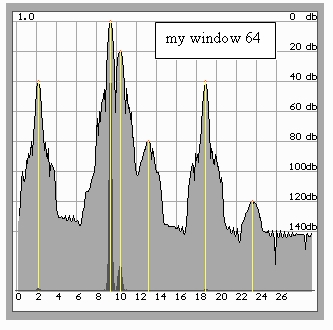
Рис.11. Ширина основных лепестков меньше, чем при использовании прямоугольного окна.

Видно, что верхняя часть лепестка сужается до совпадения с линией (обозначенной желтым цветом)

соответствующей частоте спектральных компонент заданной модели,

т.е. достигается разрешение, кажущееся невероятным в классическом спектральном анализе.

 

В результате примененного метода использования изменяющегося окна данных, поставленная данной моделью задача выделения всех спектральных компонентов решается полностью. Это совершенно невозможно при использовании классического подхода с однократным анализом реализации и при выборе любого из существующих в настоящее время окон данных.

 

Не исключено, что эта задача может быть решена также при использовании неклассических методов спектрального оценивания (авторегрессионных и др.). Однако не следует забывать, что авторегрессионные методы исследуют, в сущности, не самое реализацию, а созданную на ее основе модель, т.е. полной замены методов классического спектрального оценивания не обеспечивают.

 

Таким образом, можно предполагать, что предлагаемый автором метод существенно расширяет возможности классических методов спектрального анализа, не выходя за пределы базовой теории. Неизбежное повышение количества математических операций, необходимых для вычисления спектра (в единицы – десятки раз) не представляет собой существенного недостатка метода. Вычислительная мощность современной техники любого уровня позволяет решать и более трудоемкие задачи в реальном масштабе времени. Кроме того, из самого метода следует, что процесс легко поддается распараллеливанию и, в таком случае, расходы для обеспечения спектрального анализа будут трансформированы в незначительное возрастание стоимости аппаратного обеспечения. Отметим также, что никакого противоречия с базовым принципом неопределенности при использовании предлагаемого метода не возникает. Частотное разрешение всего лишь стремится к своему теоретическому пределу, но не превосходит его.

 

Оптимизм, однако, присущ чаще всего некомпетентным и патологически энергичным «изобретателям». Поэтому, предваряя возможную критику и подозрения в некомпетентности или клиническом дилетантизме, следует указать, что вид спектра при вычислении его с изменяющимся окном действительно получается несколько необычным. Лепестки относительно высокой энергии имеют форму, похожую на церковные колокольни – узкий верх и ступенчатое расширение внизу. В то же время низкоэнергетические компоненты такой формы не имеют, зато расширены относительно более мощных компонент. Причиной таких эффектов является использованный способ трансформации окна. Т.е. расширение окна при вставке прямоугольного участка (как будто терьер вытягивается в таксу) заведомо не является оптимальным способом трансформации. Эту задачу решить пока не удается вследствие ее значительной математической сложности. Хотя, конечно, метод оптимальной трансформации окна существует, и при его использовании все лепестки приобретут приятный для взгляда вид.

 

Практическое приложение предлагаемого метода может быть, на мой взгляд, очень широким: от спектрального анализа в радиолокации до исследования электроэнцефалограммы. Попробуем применить его к стандартной реализации ЭЭГ здорового человека. На рис. 12. показан фрагмент электроэнцефалограммы здорового человека в состоянии спокойного бодрствования с закрытыми глазами.

 

 

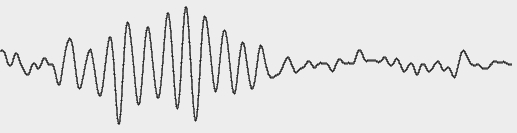
Рис.12. ЭЭГ с выраженным хорошо модулированным альфа ритмом частотой около 10 герц.

Квантование 16 разрядное, частота дискретизации 200 герц.

 

Проведем спектральный анализ данной реализации стандартным методом с применением окна Хэмминга. Спектр показан на левом изображении (рис. 13). Наглядно проявляется доминирование альфа ритма, другая ритмическая активность также представлена в полном соответствии с характеристиками ЭЭГ здорового человека.

 

На спектре, полученном с помощью предлагаемого метода, картина существенно отличается. Если основные спектральные компоненты совпадают с предыдущими данными как по частотам, так и по уровню, то минимумы спектральных плотностей отличаются весьма существенно. Поразительно, но минимумы практически точно попадают в области разделения ритмов, описываемые классической электрофизиологией. Так, наблюдается четкое разделение дельта активности (0,5-3Гц) и тета (4-8Гц). Альфа ритм также отделен от бета активности, которая в свою очередь хорошо разделена на классические бета1 и бета2. Неожиданным является лишь разделение бета1 активности на два поддиапазона.

 

  

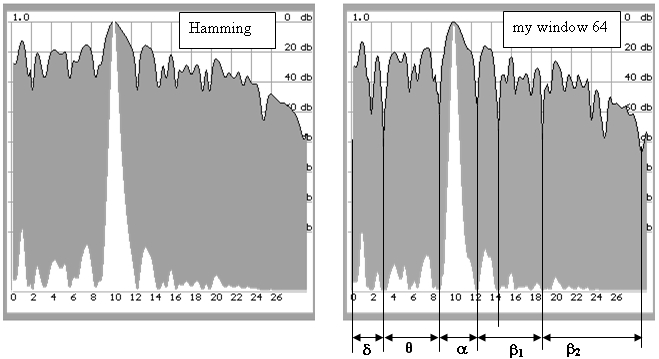
Рис.13. Спектры показанной ЭЭГ. Слева – окно Хэмминга, справа – предлагаемый метод.

 

Следует также учитывать, что зафиксированные минимумы (до –80дБ) при 16 разрядном квантовании и ненулевых собственных шумах усилителя однозначно свидетельствуют о полном отсутствии электрической активности мозга на этих частотах (т.к. шум усилителя и шум дискретизации дают примерно –80дБ, а на долю истинного сигнала ЭЭГ ничего не остается). Такой факт может представлять значительный интерес для физиологов – мозг не генерирует электрических сигналов на очень точно настроенных частотах. Т.е. либо ЭЭГ – сумма большого количества весьма частотно стабильных генераторов, либо это «фраунгоферовы» линии, обусловленные противофазной генерацией. И очень интересно, как эти минимумы спектральной плотности ведут себя с течением времени, при функциональных пробах и при различных заболеваниях. В любом случае, с помощью предлагаемого метода мы получаем новое качество анализа электроэнцефалограммы.

 

Так что, с некоторым нахальством можно предположить, что предлагаемый метод оценки спектра с изменяющимся окном данных допустимо считать развитием классического спектрального анализа.

 

  

61001 г.Харьков, а/я 11515, т./факс: (057)-7171077, (057)-7544990; (057)-7546692

 e-mail: tredex@vlink.kharkov.ua,   www.tredex-company.com