Double correlation reception of a symmetrical pulse under conditions of AWGN
12/13/2010
The optimum coherent (binary) threshold detection of a weak signal in additive noise is mainly determined by the square root from the signal-to-noise ratio at the input as to power, and the device for detection itself must determine the averaged generalized mutual correlation of the received data with the signal.
David Middleton
.
The optimum detection of a single pulse in the presence of noise consists, as to modern notions, of two parts:
- Optimal filtration, which is the convolution of received signal with its inverted in time copy.
- 2. Non-linear transformation (in the form of decision making: signal is present or not) by a threshold detector with the minimum Bayes risk, or by a device detecting the response extremum of the ideal filter.
Let us consider a classical example of detection of a symmetrical square video pulse. We shall use a specially written for this purpose application for obtaining experimental results of pulse detection on the background of white Gaussian noise.
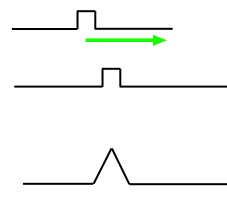
Fig. 1. Convolution of a signal with its copy in the case of zero noise.
According to the theory the system's response is a triangular pulse the width of which at the base is twice the width of the input pulse base.
In the presence of noise we obtain the following result of optimum filtration:
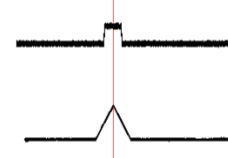
Fig.2. AWGN with the amplitude much less than the signal at 1000-fold imposition of images.
If the noise level increases, the detection of the pulse will become more and more difficult, the probability of errors of the first and second kind will increase.
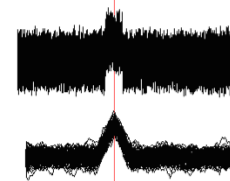
Fig.3. The noise level is comparable with the signal level.
In order to estimate the efficiency of threshold detectors of any kind (namely they are most often used in modern engineering), let us use the standard method of eye diagrams. Let us consider the extreme case, when the detection is on the edge of error appearance.
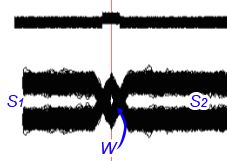
Fig. 4. Eye diagram of the optimal filter output. 1000 iterations.
It is obvious that for our case the absence of detection errors will be observed when and only when there is a non-closed eye W, and slots S1 and S2 are passable along the entire length.
Let us show that with further increase of the noise level the error-free detection of the pulse by means of this algorithm is impossible at any threshold setting.
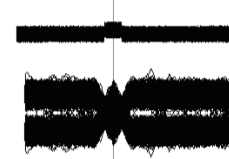
Fig.5. The noise level is increased by 3dB. The eye is absent, the slots ate impassable. It is clearly seen that under the condition of any threshold errors will appear, both of the first and second kinds.
It is obvious that in this case the theoretical limit of the possibility of pulse error-free detection is reached.
However, let us suppose that we have used not all possibilities to optimize the receiving device. In particular, we have neglected the fact that the pulse being received is a symmetric one. That is, if we reflect both its sides one onto the other in respect to the axis of symmetry, we can hope that the ratio signal/incoherent in respect to this reflection noise will be improved by 3dB (as summing of two halves of the signal is equivalent to coherent accumulation of two realizations of the same signal).
We shall demonstrate this effect on a vivid example. Let there be a photo where the image is symmetric in respect to the vertical axis. Then each line of the image will be repeated (naturally, with inversion) after the axis of symmetry.
Fig.6. Let us make the portrait of Norbert Wiener axis-symmetric in respect to the red line, that is use only one half of the image.
Fig.7. We add AWGN, the noise being without symmetry, which the initial portrait has.
Fig.8. We impose the right-hand half of the portrait on the left-hand one taking into account inversion. We can see that noisiness of the left-hand half has decreased.
Fig. 9. We multiply the obtained image by the prototype, that is we perform the operation close to the optimal filtration when receiving a pulse.
It is obvious that I this case the left-hand part of the portrait has been restored more correctly, because it has the improved by 3dB signal-to-noise ratio.
In our case it is senseless to apply such method to the input signal, as a priori we do not know the position of the axis of symmetry (that is the moment when the pulse arrives); even more, this is the purpose of operation of the entire system. The attempt to use such method will lead to "reproduction" of input pulses, widening of the system response in time and by no means will improve the signal-to-noise ratio after optimal filtration.
But nothing forbids us to use such method for the output signal under the condition that we shall calculate the correlation function with its prototype using the method of normalized correlation. Let us explain: we calculate Pearson's coefficient of correlation with sliding window, where the signals are the system response after the optimal filter (in our case – triangle signal) and prototype (that is the same triangle signal). The input signal is averaged thereat in respect to the axis of symmetry, which is defined as the center of the sliding window.
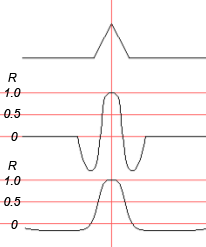
Fig.10. Pearson's signal for the sliding window equal as to duration to the input triangular pulse (second curve) and equal to the entire realization (lower curve).
Let us carry out an experiment on pulse detection under the conditions of AWGN of a low (compared to the pulse) level.
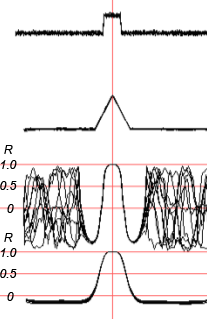
Fig.11. For the sliding window equal as to duration to the expected pulse, there are constant false rises R almost to 1.0. Although there are no errors in the vicinity of the pulse.
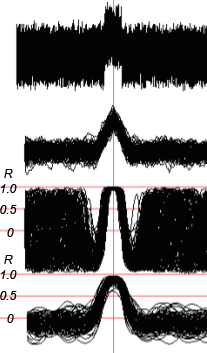
Fig. 12. For the case of high-level signal one can see that Pearson's signal is quite suitable for threshold detection of pulse.
Let us show experimentally that the proposed method of reception of a symmetrical pulse really ensures the operation under worse signal-to-noise ratio. We will use eye diagrams for that.
Fig.13. Both detectors work without errors.
Fig.14. The noise level was increased by 3dB as to amplitude. Only the proposed detector works error-free.
In order to ensure narrowing of the system response, we can use a signal for the window equal as to duration to the input pulse of the system under the condition that the correlation coefficient for the window with the duration equal to the realization, have exceeded level R=0.
As a result we can recommend the following detector structure: the signal realization obtained after optimal filtration (in our case 256 readings) is compared (that is the correlation coefficient is calculated by Pearson's formula) with the prototype, the input signal being additionally processed as follows: the input signal readings symmetric as to the prototype center are averaged. If a symmetric reading is outside the realization, the operation is not performed.
The same operation is performed with a "short" sliding window (in our case 40 readings with the input pulse duration of 20 readings). We obtain two curves (lower lines in Figs. 11 and 12). Their positive values (negative ones are zeroed) are multiplied between themselves, and we obtain a unique output signal that describes the degree of similarity of the received signal to the sample. Naturally, some marginotomy takes place – the realization "tails" are cut off by the duration of expected signal.
I take the liberty to propose to call such device a double correlation detector.
Let us consider the operation of the detector in more detail.
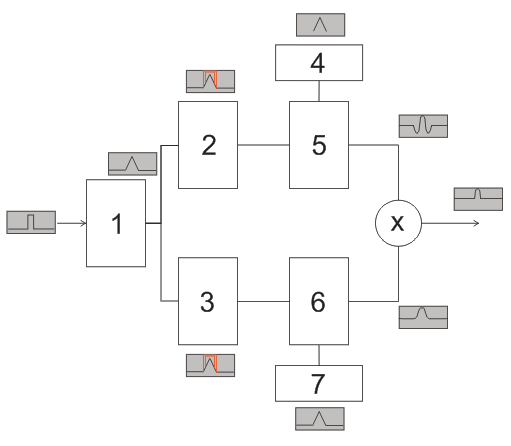
Fig.14а. Block-diagram of double correlation detector.
1 –optimal filter; 2,3 – mirror summing units; 4,7 – signal prototypes; 5 – first correlator: sliding window equal to pulse duration; 6 – second correlator: sliding window equal to realization; Х – multiplier.
1 –optimal filter; 2,3 – mirror summing units; 4,7 – signal prototypes; 5 – first correlator: sliding window equal to pulse duration; 6 – second correlator: sliding window equal to realization; Х – multiplier.
At the output of the entire system we obtain the signal shown in Fig.15.
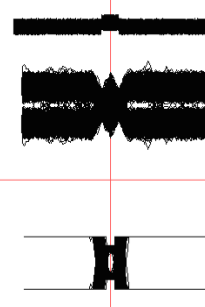
Fig.15. Eye diagram for the proposed detector (bottom). In this case the signal-to-noise ratio does not permit to avoid errors when using standard threshold devices (middle diagram).
Fig.16. Variation of the detector output signal depending on the input signal-to-noise ratio. The device behavior is very similar to "frequency catching" by a usual FM detector.
Please pay attention that the detector output signal does not depend on the level of the input one and is always within 0…1. That is the automatic gain control system can be turned off (if a required dynamic range is ensured).
It should be also noted that at coherent accumulation of signals, so called "interference burning", we can use the averaging function not at the input, but at the detector output. In this case it is possible to obtain additional information on the signal-to-noise ratio of the initial sequences and, correspondingly, to forecast the minimum necessary number of accumulation iterations.
It should be also noted that at coherent accumulation of signals, so called "interference burning", we can use the averaging function not at the input, but at the detector output. In this case it is possible to obtain additional information on the signal-to-noise ratio of the initial sequences and, correspondingly, to forecast the minimum necessary number of accumulation iterations.
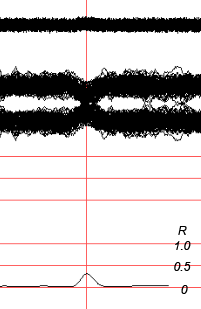
Fig.17. "Interference burning" by the method of coherent accumulation of 64 realizations. Please note that the output signal level of the detector is proportional to the input (very small, NB!) signal-to-noise ratio.
Conclusions:
- The proposed double correlation detector yields advantage of 3dB in amplitude and, respectively, 6dB in power, when receiving a single symmetrical pulse. We must suppose that this advantage will be of the largest demand in radar systems, as it is possible to obtain the gain equivalent to the double increase of the transmitter power.
- The normalized output signal proportional to the degree of similarity of the received pulse to the sample one makes it possible to perform optimal detection regardless the input signal level, which favorably distinguish it from threshold detectors.
- On the basis of the proposed device one can design not only detection systems, but also systems of recognition of various input signals; to do this it is necessary to compare not with one, but with several prototypes. In this case it is possible to realize the principle of optimal receiver, which does not require AGC systems.
- Understanding that I should send all this to a peer-reviewed publication, but being reluctant to do so, I hope that competent readers will help me with constructive criticism.
Category:
- Log in to post comments
|
|
|